The simplest method to determine the probability associated with a z-score is to reference the corresponding probability in the z-table. This guide demonstrates how to employ the z-table to ascertain the probabilities of:
- A value being below a specified z-score.
- A value exceeding a specified z-score.
- A value falling within the range of two specific z-scores.
Calculate Probability for Values Below a Specific Z-Score
Let’s assume we want to calculate the chance that a value from a particular distribution falls below a z-score of 0.55.
To ascertain this probability, we reference the z-table for the entry corresponding to 0.55:
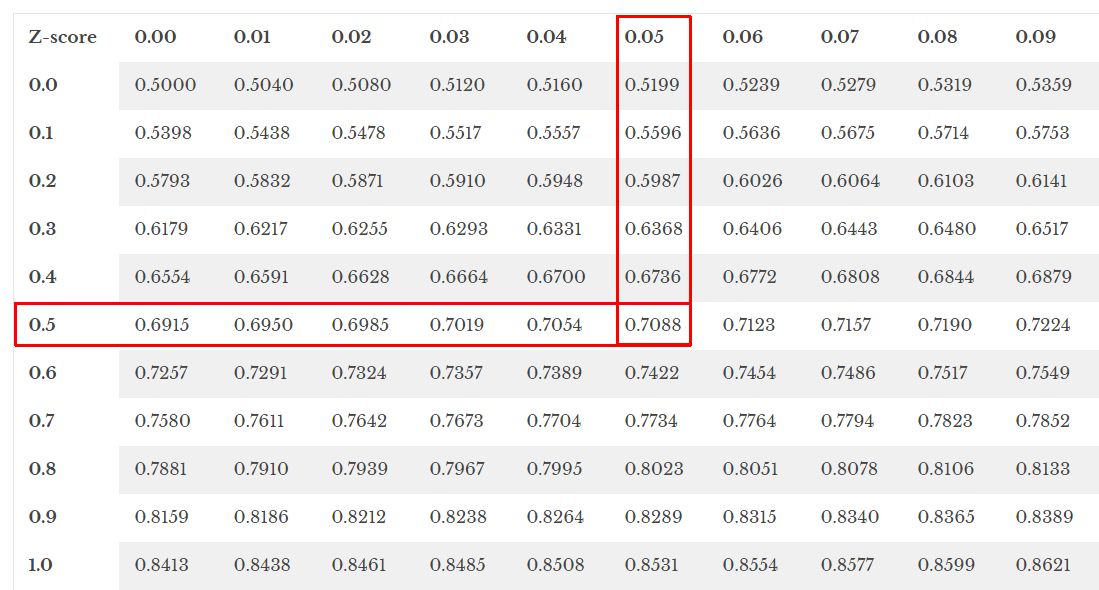
The probability of a distribution value being less than a z-score of 0.55 is roughly 0.7088.
This probability can also be represented as 70.88% when converted to percentage form.
Note: Check out our Z-score calculator if you don’t have the Z-score.
Calculate Probability for Values Above a Specific Z-Score
Consider the task of finding the likelihood that a value from a distribution exceeds a z-score of -1.2.
We look up the value -1.2 in the z-table:
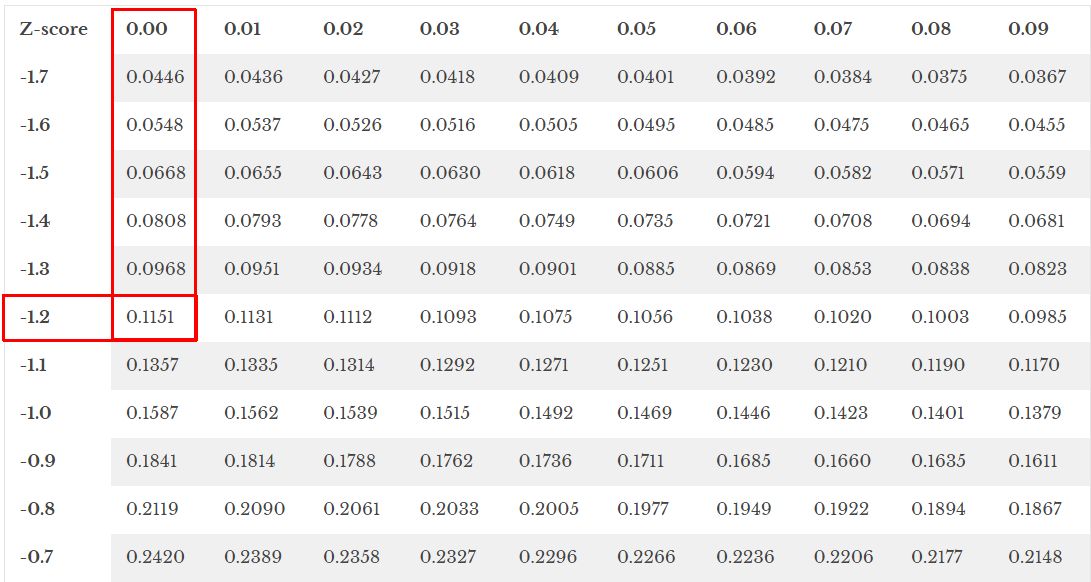
The z-table lists a probability of .1151 for a z-score of -1.2.
To find the probability of a value being greater than this z-score, we subtract the table value from 1:
Thus, the probability of a value in the distribution exceeding a z-score of -1.2 is 1 – .1151 = 0.8849.
Calculate Probability for a Value Within a Range of Z-Scores
Imagine we need to find the probability that a value’s z-score is between 0.25 and 0.97 in a certain distribution.
Initially, we find the z-score of 0.25 in the z-table. Subsequently, we look up the z-score of 0.97.
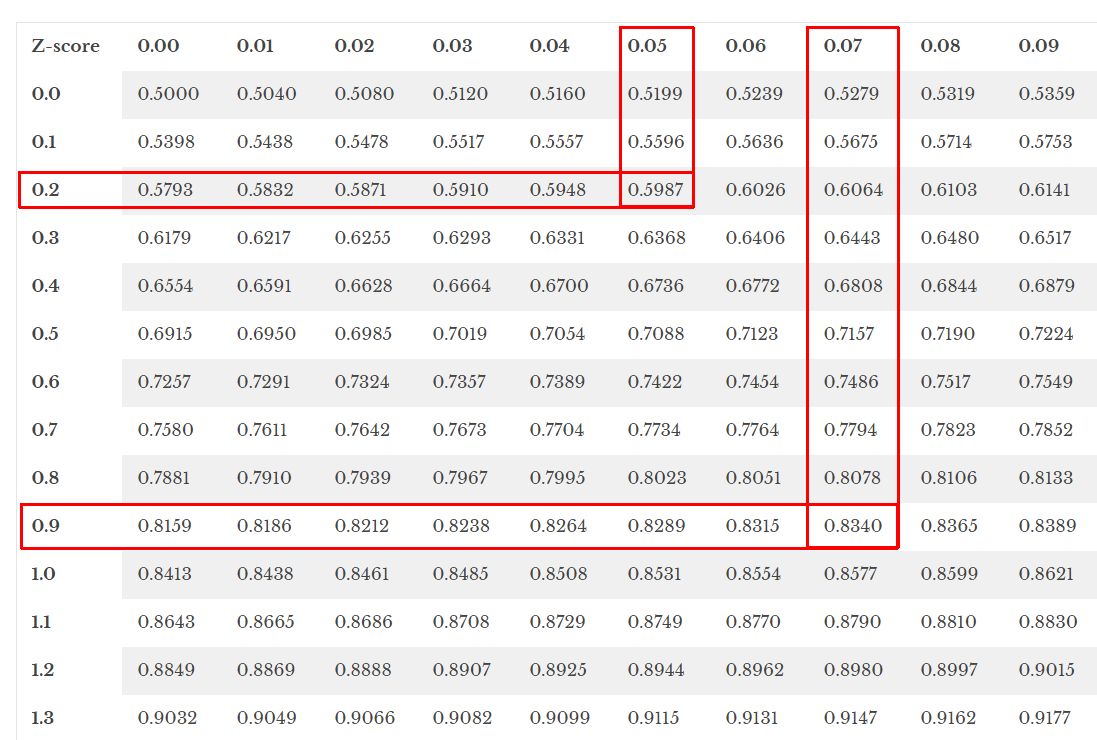
To calculate the probability, we subtract the smaller value from the larger one: 0.8340 – 0.5987 = 0.2353.
Therefore, the probability that a value in the given distribution has a z-score between 0.25 and 0.97 is approximately 0.2353.
Note that this can automated and you can use our calculator to find the area between two Z-scores.