When you hear the term “slope” what comes to mind? Do you think of someone skiing down a large mountain? Or, do you think of the slide at the playground? Regardless of what you are thinking, it is likely going to be something on an incline. When you study slope in Algebra, you are studying the incline along with other characteristics of a line.
Learning the proper way to calculate slope is a simple process when you know exactly what the “slope” means. In a nutshell, the slope of any line is the change in the y-values versus the change in the x-values.
When you begin calculating slope, you may find the process a bit confusing because lines are given in several different forms. For example, you can calculate the slope from the graph of a line, equation of a line, table of points to the line or when you are given any two points on a line.
What is Slope?
Before you dive in to find the slope of a line, you should understand exactly what this term is referring to. Slope is used to determine the steepness of a line and it can be used to show how much something changes over time. Slope is calculated with a simple algebraic equation.
Slope is defined as the rise over the run. It is written in fraction form, as follows:
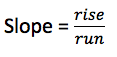
4 Steps to Calculate Slope
The slope of a line can be determined with the following four steps.
Step 1: Find two points anywhere on the line.
Step 2: Count the rise (the units up or down) to get from one point to the next. This is the numerator.
Step 3: Determine the run (the units left to right) to get from one point to the next. This is the denominator.
Step 4: If possible, simplify the fraction.
Helpful Tip: If you count right or up the number will positive. If you count left or down, the number is going to be negative.
Solve for Slope with Two Points on a Line
When you are given two points, you can easily determine the point of a line; however, it is essential to label the numbers properly. For example, the first point is displayed as (x1, y1) and the second point is written as (x2, y2).
This means that x1 is the first value of x given and x2 is the second. The same goes for the y’s.
Once you have your points, which for this example will be (7, 8) and (4, 2) you can plug it into the formula for slope.
To determine slope when you are given two points on a line, there is an easy equation to use, which is:
Y1 – y2/x1 – x2
For the example, you would plug in the given numbers to have the following equation to solve:
8 – 2/7 – 4
This equals 6/3 and can be reduced to 2. This means the line has a slope of 2.
With the information here, you are well on your way to calculating the slope of any line, easily and without hesitation.