Every creature on Earth shares a certain common bond. It’s not a complicated, deeply hidden element or some other-worldly connection; it’s just a simple truth. We all enter into existence at some point, and we all leave our existences at another point down the line.
In between those beginning and ending points, we each have our own experiences. Some are shared with other people whereas others are purely internal, but they all affect us in one way or another. Are all these events purely random, or is there some rhyme and reason behind them?
Many philosophers, teachers, mathematicians and life-livers in general believe nothing is random. A man born in Italy more than 800 years ago falls into this category. His name was Leonardo Pisano Bogollo, but today, we know him as Fibonacci. He developed a love of numbers at a young age, and this passion led to a discovery capable of changing the way people look at life and the world around them.
The Fibonacci Sequence Comes to Life
Some believe if you look closely enough, you can find a pattern in anything. This may very well be true, but Fibonacci was able to pull a specific pattern from his knowledge of numbers and prove it could, conceivably, go on forever. He pointed out the Fibonacci Sequence in his first book, Liber abacci, where he posed a mathematically based word problem for all to ponder.
“A certain man put a pair of rabbits in a place surrounded by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair from which the second month on becomes productive?”
This may be a good time to make a pot of coffee and nail down the whereabouts of the aspirin because your mind is about to be blown!
Okay, here we go! See, Fibonacci reasoned the rabbits would reach maturity and mate in about a month, so after one month passed, there was still only one pair of rabbits. Since their gestational period is also a month, the second month came to an end with still only one pair. At the end of that third month, though, a second pair made its appearance. Female rabbits should be able to give birth once a month after their first litter, so month four saw the first pair produce another.
Month five rolled around, and pair one reproduced again while pair two did the same. At this point, the grand total was five pairs. Long story short, at the end of the year, 377 pairs lived within the confines of the wall.
Looking a Little Deeper
Granted, Fibonacci made a few pretty bold leaps before forecasting the fruitfulness of this fluffle. His scenario revolved around some highly controlled conditions. For instance,
- Each new litter consisted of two rabbits: one male and one female
- All were physically capable of reproduction
- Each female was able to begin the reproductive process at one month of age and give birth to a new litter each month thereafter
- All made it through the entire year without succumbing to illness or being kicked out of the compound by the other rabbits
In truth, some rabbits can take four months or more to reach maturity. Up to 12 offspring can be born in a single litter, and not all are guaranteed to survive. When you really think about it, though, uncontrolled numbers and natural selection could certainly offset each other. Fibonacci’s well-thought-out conditions might easily account for all the possibilities and balance the scales.
Breaking it down
All these ideas may sound a bit abstract in written form. Of course, Fibonacci’s math is spot-on. Once you put the numbers where the words are, it becomes a little clearer. In the Fibonacci Sequence, you begin with 0 and 1, and move on from there. Simply stated, it goes like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 and so forth.
Each new number in the sequence is created by adding together the two previous numbers.
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
13+21=34
21+34=55
34+55=89
You could go on indefinitely, adding together the last two numbers in the sequence to reveal the next. While the explanation sounds drawn out and complex, it’s really fairly simple. Matters get quite a bit more involved from this point, though.
The Concept Takes Shape
We’re about to take this thing to a whole new level here. Imagine the numbers in the Fibonacci Sequence represented by squares like those on a piece of graph paper. Find a starting point somewhere near the center of the page, and color in a single square representing the first number in the sequence (1). Next to it, do the same in honor of the second one. Then, with two being the third number, use a different color to shade in a 2 by 2 square space. From there, find a different hue to color in a space measuring 3 by 3 squares and so on. You’ll end up with a vibrant version of this example:
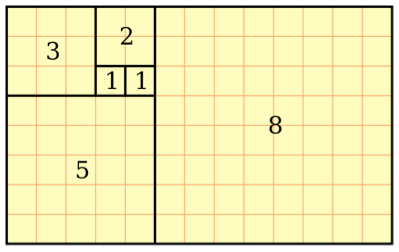
Do you notice how they fit perfectly together like pieces of a puzzle? The next number in series would be 13, and the figure taking shape here happens to measure 13 squares across. As you work your way through the larger numbers, the pattern stays the same. Each new square will be larger than the next, but following the numbers in the Fibonacci Sequence, they’ll always click neatly into place in exact proportion to the ones before them.
Now, if you’re following along on paper, grab a pen. Start in the upper corner of your first single square, and draw the first stage of a spiral running to its opposite corner, cutting the square in half. Continue your line across the next single block and on through the following ones, drawing your spiral across the diagonal center of each larger square. You’ll end up with something like this:
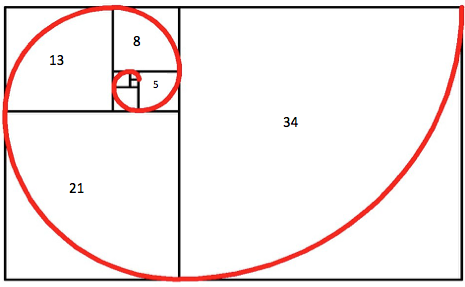
Fibonacci’s spiral and the rectangle created by his sequence of numbers are known as the Golden Rectangle because of their connection to the Golden Ratio. As a number, this magical figure is 1.61803, and it’s represented by the Greek letter Phi (Φ). It may start to seem like we’re jumping around a bit, but all this really is relevant.
In geometry, the Golden Ratio is created when you divide a line into two pieces, but not just any two pieces. The line has to be split in just the right place where the entire line divided by the length of the longest portion of its division is exactly equal to the longest segment divided by the shortest one. You guessed it: both figures must equal 1.61803.
Rectangles created using the Golden Ratio are said to be the most pleasing ones you’ll ever see. This brings us back to Fibonacci. As it turns out, when you take any two successive numbers in his sequence and find their ratio by dividing the larger one by the smaller one, it’s extremely close to the ancient golden standard. Watch this!
21/13 = 1.61538
89/55 = 1.47272
121393/75025 = 1.61803
Look at that! We found a winner! Having said all that, the Fibonacci Sequence, the Golden Rectangle and its inherent spiral are all around us. You’re on the verge of finding out how and where.
Spiraling into Complete Control
Before you read any further, you need to make absolutely sure you’re ready to make this leap. This is just a little friendly advice. Once you see it, you can’t un-see it, and it’s life changing!
The Golden Rectangle generated by Fibonacci’s Sequence has been making appearances around the world for centuries. One prime specimen is the Parthenon in Greece. Numerous instances of the Golden Ratio and Rectangle are found inside and out in both large and small scale.
Leonardo da Vinci’s Mona Lisa could be considered another display of the near-Golden Ratio at work. Its dimensions are said to be 30 inches by 21 inches. When following the standard plan, the larger side of the rectangle divided by the smaller one comes to 1.42857. It’s not an exact match, but it’s close.
Heading to Egypt, we find another possible example in the Great Pyramid of Giza. The largest of the three pyramids, this one measures 756 feet wide and 481 feet tall. When you do the math, the ratio is 1.57172; again, it’s right on the border line.
Artist Piet Mondrian inserts the Fibonacci Sequence into some of his paintings as well. You can clearly see the puzzle-piece squares making up the Golden Rectangle in certain examples of his work. If you look at it long enough, your mind’s eye may even begin drawing in the spiral.
These are only a few widely known cases of this pattern being worked into art, architecture and engineering over the centuries. Plenty of people insist it’s mere coincidence, referring back to the fact you can find patterns in almost anything if you’re looking for them. Along those same lines, some of these instances came into being long before Fibonacci himself.
Many chalk it all up to the obvious. Some of the brightest and most aesthetically inclined minds in history are behind the making of those productions. Pure logic dictates they’d incorporate the most visually pleasing dimensions into their work even if it’s on a subconscious level.
You can rationalize the situation in any number of different ways, but it runs even deeper still. Certain things can’t be ignored or explained away.
It’s Only Natural
If you step outside and look around, you’ll also find Fibonacci in nature, and it’s not in only one or two different places. Sunflowers are a prime example. Those brilliant yellow petals surround a large mass of seeds, but the seeds aren’t arranged in some haphazard manner; they coil gracefully out from the center of the seed head.
Pine cones are another widely used case in point. You’ll notice their spikes are arranged in spirals from both clockwise and counterclockwise perspectives. The same is true of pineapples. If you have a holly bush nearby or some similar type of shrubbery, take a look at it. At first, the leaves appear to grow randomly or even in circular patterns. Upon closer examination, you’ll see they’re actually staggered a bit, running in rough spirals from tip to trunk.
Mankind also exhibits little snippets of the Golden Rectangle. Average adult human faces measure eight to nine inches long by six to seven inches wide. If you work out the ratio of the two extremes, it comes to 1.5, which is within a fraction of the Golden Ratio. Human hair tends to grow outward in spirals from a central point. From here on out, you’ll start seeing version of the sequence everywhere you look. Don’t say we didn’t warn you beforehand!
Doing the Math
As is the case with most mathematical situations, there are rules for calculating numbers in this series. It comes complete with its own variety of formulas. First off, let’s look at a demonstration of the general rule surrounding the Fibonacci Sequence:
xn = xn-1 + xn-2
Here, “n” gives each number in the Fibonacci Series a corresponding number in our traditional sequence: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
“Xn” represents the numbers in the Fibonacci Sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Using the rule, we can calculate a number in the sequence. Let’s try the seventh one:
x7 = x7-1 + x7-2
x7 = x6 + x5
x7 = 8 + 5
x7 = 13
It’s really just another way of saying, “A specific number in the Fibonacci Sequence is equal to the sum of the two numbers before it.”
From here, it only gets more complex and involved. You’ll find any number of equations and explanations surrounding mathematical induction, linear recurrence, plotting the sequence on graphs, etc.
These formulas are Greek, if you’ll pardon the pun, to those who try to jump head-first into the advanced end of the spectrum. Unless you have some background on the actual problem-solving techniques at work here, it’s best to ease into the situation. Once you understand the basics like the formula above, it’s a simple matter of taking baby steps thereafter.
Overall
We all have common bonds. Whether they’re random and coincidental or products of underlying mathematical sequences and mysteriously ordered chaos is largely a matter of opinion. No matter where you stand on the issue, certain patterns can’t be overlooked or easily dismissed. Fibonacci saw this even as a child, and his life’s work set off an unstoppable sequence of events.