In math, geometry is the science of finding the measurements of shapes. There are several different measurements that can be calculated depending on the type of shape. These measurements are called dimensions. Width, depth, or height are examples of dimensions.
Shapes can be broken into planes, geometric figures, or even just a point. Planes only have two dimensions such as length and width. Three-dimensional shapes have length, width and height. A point would only have one dimension. While a point doesn’t take up enough space to calculate for, planes and geometric figures do. This means planes and geometric figures have an area that can be calculated.
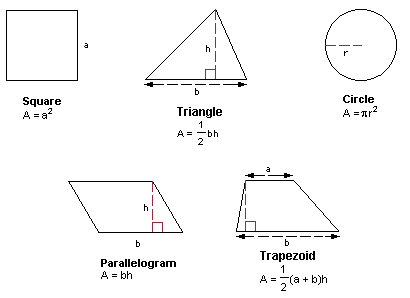
For each shape, there is a different formula to find its area. Three-dimensional shapes have surface area since space inside them will need to be calculated differently. The area inside a three-dimensional shape is called volume. Since calculating three dimensions is much more complex, it’s easier to focus on learning how to find the areas of two-dimensional shapes first.
Dimensions of Plane Shapes
A two-dimensional shape does not have volume, so calculating the area inside that shape is much easier. Depending on type of shape those dimensions have different names to make them distinct and avoid confusion when making measurements. For example, a square has length and width while a triangle would have base length and perpendicular height.
To make things clearer when measuring less conventional shapes, the angles along the perimeter of the shape also have names. A right triangle has a right angle, a curved triangle has both a rising and falling angle.
Measuring Areas
The measurements along the outside of the shape are taken in regular units. However, the area is measured in square units to account for volume. Regular units only measure in a straight line, squared units’ measure over an area. Squaring a unit of measurement is simple, it just needs to be multiplied by itself.
Squares are considered the most basic shape, so they have the most basic formula, S2. The variable of S stands for the measurement of one side. So, the area of a square can be found by measuring one side and multiplying it by itself. If the side of a square is five centimeters, the area of the square is twenty-five square centimeters.
Even though a rectangle also has flat sides, the formula is different. Multiplying the length and width will give the area of a rectangle.
Measuring the area of curved shapes is a little different. For irregular shapes, such as a lawn, control points can be created. This is done by finding the widest points of the shape and measuring to the opposite side. The measurement in between is called a line segment. These lines can have specific names. For example, a line that only goes half way across is called the radius. This line segment can be used to find other measurements in the circle. The diameter is found by multiplying the radius by two.
When measuring the area of curved shapes Pi will most likely be used in the formula. To find the area of a circle the formula is 2x Pi x radius. With a radius of four centimeters, the formula would be 2x 3.14 x 4 with a solution of 25.12 square centimeters.
For each unique shape, the formula to find its area will need to be used. There are dozens of formulas for finding area and each can be useful in its own way.
By finding the correct formula solutions to real world problems can be found easily.