The Law of Sines, also sometimes called the Sine Rule, is one of the most useful mathematical laws when it comes to solving triangles. It can be used to help find both unknown angles and unknown sides with ease, and will work for any given triangle. This simple mathematical law states: a/sin A = b/sin B = c/sin C.

Some students may be scratching their heads right now and thinking, “that’s simple?” Once it has been dissected into plain English, the answer is yes! Take a look at the graphic above, but note that the angles and sides could have any measurements and it could be any triangle. Now take another look at the law. The numerators “a,” “b,” and “c” are all sides. The denominators “A,” “B,” and “C,” are their corresponding opposite angles. So, when broken down into layman’s terms, if the side of a triangle “a” is divided by the sine of its opposite angle “A,” the result will be equal to side “b” divided by sine “B,” and also side “c” divided by sine “C.” See? Not as complicated as it sounds.
How to Use the Law of Sines
If any one angle and corresponding opposite side of a triangle are given, and either the side or the angle of another side is also given, it’s easy to find the missing information using the Law of Sines. The best way to understand how is to give it a shot using an example. Take a look at the triangle below. We’re going to solve for side “c” using what we’ve learned.
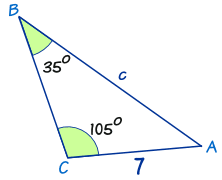
The first step to take is to identify which corresponding angle and side are already given. In this case angle B, which measures 35o, and its corresponding side b, measuring 7, are our only starting point. The next step is to plug all of these numbers into the equation provided above in order to identify which information is missing. It would read: a/sin A = 7/sin(35o) = c/sin(105o).
We’re going to solve for side “c.”
Basic algebra tells us that we need to rearrange the equation in order to isolate the variable we are solving for. For the purposes of this example, ignore “a/sin A” entirely, as it doesn’t offer any useful information. Isolating the variable “c” requires that we multiply both sides of the equation by sin(105o), leaving us with: c = (7/sin(35o)) x sin(105o).
Next, replace the values for sin B and sin C with numerical estimates. The sine of 35o is roughly 0.574, and the sine of 105o can be estimated at 0.966. This leaves us with c = (7/0.574) x 0.966, or 11.8 if rounded to the first decimal place.
The exact same process can be used to solve for unknown angles as well. Simply find the angle and corresponding side with known values, and the angle that is being solved for. Enter these into the equation above, isolate the variable, and inverse the sine to get the final answer.
Solving for the other unknown side or angle requires one more bit of basic knowledge: all of the angles in any triangle always add up to 180o. With that important fact in mind we can simply subtract the two known angles from 180o to find the third, plug this information into the equation as above, and find the final side.