Asymptotes are used to help students in graphing rational functions. There are three different kinds, but the most common, and simplest to understand, are Horizontal and Vertical Asymptotes, so let’s start there. An asymptote is defined as a line that is approached by a curve as it approaches infinity. The direction of these lines can be either positive, or negative, but in order to be considered an asymptote the distance between the line and the curve has to tend to zero.
As implied, a horizontal asymptote functions on the horizontal, or “x” axis.
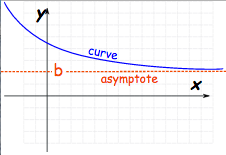
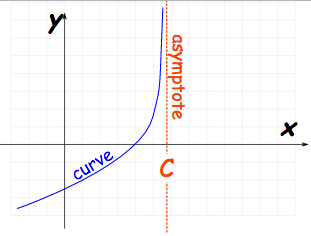
A vertical asymptote functions on the “y” axis.
The third kind of asymptote is called an Oblique Asymptote. Instead of mirroring either the “x” or the “y” axis, oblique asymptotes follow the formula “y=mx+b” as the “x” approaches infinity.
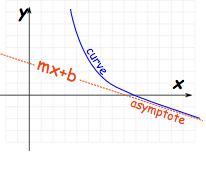
That’s a little bit more complicated, right?
It’s probably time to take a few minutes to evaluate the uses of asymptotes of all kinds. As noted above, they are useful in graphing rational expressions. A rational expression expresses a ratio between polynomials. It’s like a fraction, except with polynomials. Like an ordinary fraction a rational expression contains both a numerator and a denominator. Here’s an example: f(x) = (x2-3x)/(2x-2). Both the numerator and the denominator of this expression contain polynomials, making it a rational expression.
Now, when these expressions are visually represented on a graph, they can have any number of vertical asymptotes. However, they can only have one or zero horizontal and oblique asymptote. The first step to take toward finding the value of any asymptote is to reduce the expression to its lowest terms. The next step will depend, though, on what type of asymptote the student is trying to find.
Finding Horizontal Asymptotes
In the cases of both horizontal and oblique asymptotes, they will be determined based on the degree of the bottom polynomial vs the top. If the top is less than the bottom, there will be a horizontal asymptote at zero. That’s fairly straightforward. If they are equal, the asmptote will be set by each polynomial’s leading terms. Since this can get just a bit more complicated, let’s look at another example: f(x) = (3x+1)/(4x+1). No matter the value of “x,” the asymptote can be defined by ¾, since those are the polynomials’ leading terms.
In cases where the degree of the top polynomial is 1 greater than that on the bottom an oblique asymptote will be produced. These require the use of polynomial long division to find an equation for the line, which may be best left for another lesson. When the degree of the top polynomial is greater bymore than 1 degree than the bottom, though, there simply is no horizontal, or oblique, asymptote.
Finding Vertical Asymptotes
Vertical asymptotes occur when the bottom polynomial in a rational expression is equal to zero. For example: f(x) = (x2-3x)/(2x-2). Since the vertical asymptote is dependent only on the denominator, that’s what we’ll focus on: (2x-2) factors into 2(x-1), which places a vertical asymptote at x=1, since 1-1=0.
Understanding asymptotes and rational functions can certainly be a challenge, but get enough practice with a graphing calculator, and eventually it’ll be easy!