Logarithmic functions need to be graphed and the process can look a little intimidating, especially if you have never worked with these functions before. For this math function, you will need your trusty pencil, a good eraser, and graphing paper. Although it seems a little scary, it is honestly not all that bad once you get the hang of them. It especially not as scary as when your sister tries to cook dinner!
Logarithmic functions are the inverse of exponential functions y = a is the logarithmic function while
x = ay is the exponential function. It is important to remember a must always be greater than 0 and must not be a negative.
There are three main properties of logarithms and they are as follows:
logb(xy) = logbx + logby
logb(x/y) = logbx – logby.
logb(xn) = n logbx.
These very basic properties of logarithms follow the principle that a logarithm is an exponent. The first property means the log of a product is equal to the sum of the logs of the factor.
The second property has a definition of the log of a quotient is equal to the difference between the log of the numerator and denominator.
The third property means the log of a power is equal to the power multiplied by the log of the base.
Okay, by now you may be stressing just a bit because these properties seem a little tough to manage. To simplify things a bit, you will need to remember a logarithm is simply the power to which a number will need to be raised in order to get another number.
There are many logarithm rules and they can be difficult to understand if you do not fully know them in their correct form. Here are a few examples of some of the rules you will need to know:
Logarithm product rule is logb(x ∙ y) = logb(x) + logb(y)
Logarithm quotient rule is logb(x / y) = logb(x) – logb(y)
Logarithm power rule is logb(x y) = y ∙ logb(x)
Logarithm base switch rule is logb(c) = 1 / logc(b)
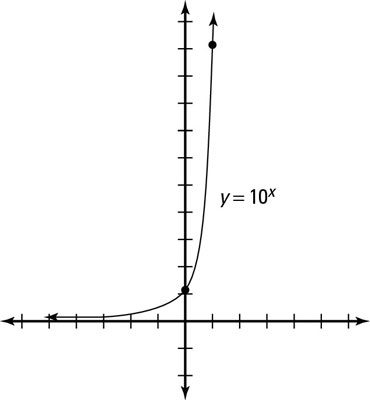
When graphing logarithms, you will first need to change the log into an exponential expression. It is important to remember the exponential expression is the inverse of the log. Here are the steps involved:
- Change the log to an exponential.
- Find the inverse function. (You will do this by switching x and y.)
- Graph the inverse function, going by the example below.
Now, that does not look too bad, does it! Working with logarithms takes practice so do not fret if you cannot seem to understand all the rules and properties right away. With continued practice, you will be able to master this function.
Fun fact about logarithms:
John Napier was the first to publicly introduce logarithms in his book, Description of the Wonderful Rule of Logarithms. This new function discovery extended way beyond the traditional realm of algebraic methods. This method became more widely recognized than previous types such as the prosthaphaeresis.