Properties of Circles
Everyone knows what a circle is. We see them every day throughout the world. What we might not see is how important circles are and how the distinct properties of a circle make it useful in a variety of ways. To understand how this unique shape can be used to solve problems and understand the world around us, it’s important to understand the properties of a circle.
A circle is defined as a shape with equal distance to all points from its center. There are no corners, thus forming a round shape. To distinguish circles from each other they can be named by the point at their center.
Circles come in any size and can be further distinguished by determining the area and transversals.
Area of A Circle
The radius, diameter, and circumference determine the area of a circle. Circumference is the area of the outside of a circle and can be found only by first finding the diameter and radius of the circle. Radius is found by measuring from the center of the center to the outside and diameter is found by measuring the distance across the middle, or with the equation R x 2 = D
Circumference is a little more difficult to find. First, it’s important to understand Pi. For basic math problems, Pi has a value of 3.14. However, the full value of Pi is yet to be determined since it is believed to be an infinite number. To find the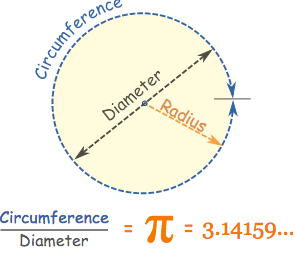 
circumference of a circle, the equation of 2π x R = C
It should be clear that the radius of a circle is the most important measurement. Finding this measurement makes it possible to determine any other geometric property of a circle by using the correct equation. This is proven further when we try to find the area of the circle. The area is found using the equationπ x R2.
Transversals of A Circle
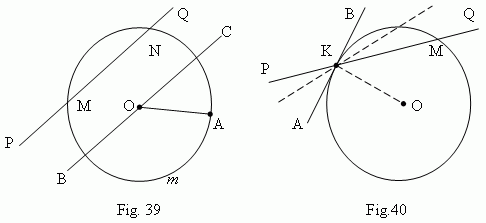Because circles are a group of points of equal distance originating from a center point, it’s possible to determine angles and lines within a circle. These lines are called transversals. To be clear, transversals are defined as a line that intersects two or more lines and can exist within a circle or be used to find a circle.
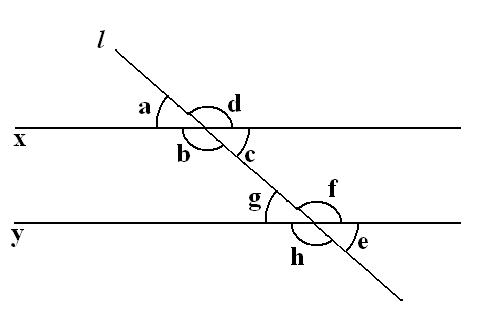Transversals are used to measure and define angles within the series of lines. By measuring these angles the geometry of circles can be found.
A circle is three hundred sixty degrees, a half circle is one hundred eighty degrees. The measurement of angles created by intersecting transversals will always produce a circle, but the intersection may not necessarily be at the center of the circle.
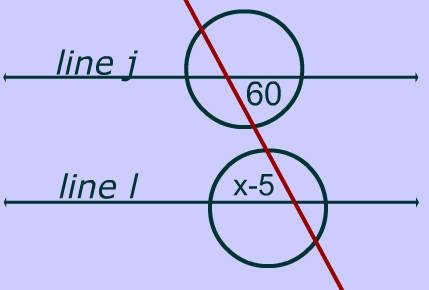Alternately, transversals can be created to find the area of a specific section of the circle.
By finding the transversals and measuring angles, it becomes possible to find and measure a circle. Simply put, the intersecting lines are measured to determine the geometry of the circle. There are three sets of angles that can be measured. Corresponding angles exist on the same areas of the lines. Alternate interior angles are on the opposite areas of the lines between the two lines. Alternate exterior angles exist on opposite areas outside of the lines.
Measuring these angles proves the existence of the circle and can be used to find every geometric aspect of that circle by using the corresponding data within the correct equation once the radius has been measured.