In math, every shape has a name that distinguishes it from other shapes. Instead of just triangles, there several types of triangles. For example, an equilateral triangle is distinct from a scalene triangle. There are names for types of shapes as well. Any shape with three or more flat sides and angels is called polygon.
Polygons are flat shapes, they only have width and length. The word polygon comes from the root words of poly, meaning many, and gon, which means sides.
The distinguishing aspects of polygons set them apart, but they all fall under the same definition. All polygons are two-dimensional shapes with flat sides and are formed of straight lines that make a closed shape.
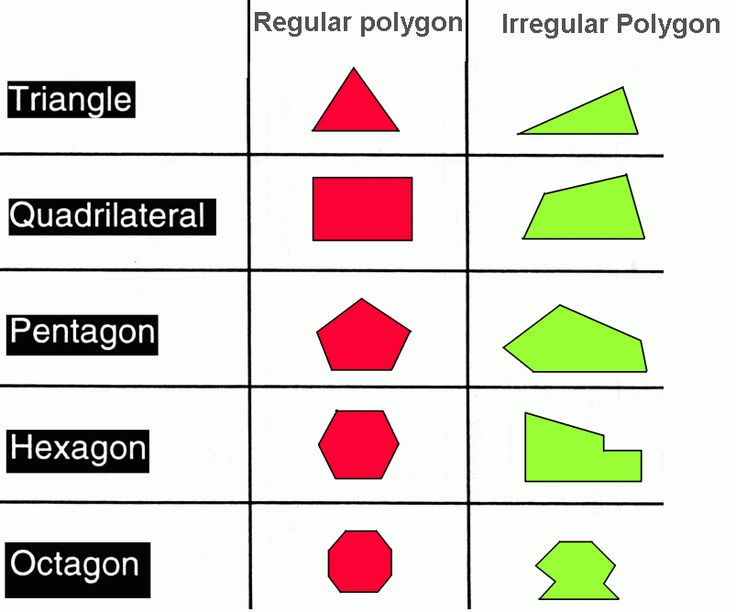
Regular polygons have equal sides, irregular polygons have some sides that are longer than others.
They can also be concave or convex and simple or complex. Each of these types of polygons has a definition that sets them apart from other shapes. There’s an exhaustive list of polygon names and definitions.
Measuring Polygons
Polygons may seem like a complex type of shape, but they aren’t. The formulas to find the area of a polygon are simple and only require basic math to solve. For example, measuring the perimeter of a regular polygon is as simple as finding the length of one side and multiplying it by the number of sides.
By finding the apothem of the shape, a formula to calculate the area can be set up. The apothem is the measurement from the center to one side of the polygon. The radius can be found by measuring from the center to a corner, or vertex.
The formula to find the area of a regular polygon is A = ½ perimeter x apothem.
Plugging in the measurements of a pentagon with sides measuring eight inches will give the area. A perimeter of 40 and an apothem of 8 would look like this, A = 1/2 (40 x 8). The area of the polygon would be 160. Irregular polygons and more complex shapes will require different formulas to solve for, but the same principles apply.
Irregular and Complex Polygons
Unlike regular polygons, complex and irregular polygons don’t have sides with the same length. This means measuring one side the multiplying the length by the number of sides won’t give the perimeter.
For irregular polygons, start by measuring the length of all the sides. Finding the sum of lengths and dividing it by the number of sides will give the side length.
The side length can then be used to calculate the perimeter by multiplying it by the number of sides. If the side length is 8 inches and there are 5 sides the perimeter would be 40.
Complex polygons can be solved for similarly, but there are a few extra steps. The lines that make up a complex polygon often intersect and create several other shapes. These extra shapes will need to be separated and measured.
By converting the measurements of irregular and complex polygons, the problem becomes solvable with simple formulas.
To find the apothem of either perimeters, the data will need to be plugged into the shape of a regular polygon. The perimeter can be divided by the number of sides to find the side length of a corresponding regular shape, such as a pentagon. The formulas used to find the apothem and area of the shape can now be used to solve the measurements of the irregular or complex polygon.