Triangles are two-dimensional shapes made up of three sides and three angles. Though not all of them are the same, they all have to have those two elements in place in order to be a triangle. You’ll run across several different types, each one defined by its sides and/or angles.
- Acute: In an acute triangle all three angles are less than 90 degrees.
- Obtuse: Obtuse triangles have one angle measuring more than 90 degrees.
- Right: A right triangle has one 90 degree angle.
- Equilateral: Equilateral triangles have three equal sides and three equal angles.
- Scalene: With a scalene triangle, you’ll have no equal sides or angles.
- Isosceles: Isosceles triangles have two equal sides and two equal angles.
With any triangle, no matter which type it is, all three angles will add up to 180 degrees. You can use this fact to find the measurement of missing angles. For example:

In this triangle, you know one angle is 85 degrees, and the other is 65. The sum of the three angles must equal 180 degrees, so:
85 + 65 + x = 180
150 + x = 180
150 – 150 + x = 180 – 150
X = 30
Geometry also gives us rules for finding the area of a triangle. Your formula for finding the area is ½ of the base multiplied by the height, or ½ x b x h = A. The base is the bottom edge of the triangle, and the height is a vertical line running from the base to its opposite angle at 90 degrees.
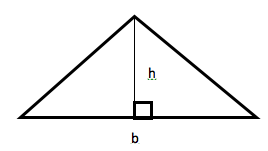
Say the base (b) of this example triangle is 72, and the height (h) is 50. When you insert those numbers into your area (A) equation, it looks like this:
½ x 72 x 50 = A
Then, if you continue to work through the problem to find the area, you’ll proceed through the following steps:
½ x 3,600 = A
A = 3,600 x 1/2
A = 1,800
Remember, always multiply the base by the height first. Then, multiply that number by ½. You can also think of it as dividing b x h by two.
Congruence
Two triangles are considered congruent if their sides and angles are identical. It doesn’t matter if they’re flipped sideways, upside-down or mirror images of each other: they’ll still have the same measurements. Five Congruent Triangle Theorems have been created over the centuries, and you can use them to find out if two triangles are identical or draw a triangle that is congruent to one you already have on paper.
- Side-Side-Side (SSS): If all three sides of two different triangles are the same, their angles will be as well, so they’re congruent.
- Side-Angle-Side (SAS): If two sides of a triangle and the angle formed where those sides meet are identical to those of another triangle, the triangles are congruent.
- Angle-Side-Angle (ASA): If two angles and the side connecting them measure the same in two separate triangles, they’re congruent.
- Angle-Angle-Side (AAS): When two angles of one triangle are identical to two angles of another and one side of each of those triangles measures the same, you can bet they’re congruent.
- Hypotenuse-Leg (HL): This theorem only applies to right triangles, or those with one 90 degree angle. When the hypotenuse, or longest side, and another side of two triangles are the same length, the triangles are congruent. You already know the angles across from the hypotenuses are identical.
Anytime you use one of these rules to prove two triangles are congruent or build your own congruent model, you can rest assured any sides or angles not covered by the theorem are going to be identical.
A triangle is essentially a sum of its parts. You can use those parts to build identical triangles, confirm two are already identical or prove they’re not identical at all no matter how similar they look. Missing angles aren’t a problem at all because you can use the ones you have to find the one you don’t. All that being said, have fun with those three-sided, three-angled shapes, and don’t let those missing links intimidate you!