The Pythagorean Theorem: Finding the Missing Length
Geometry began to take shape thousands of years ago. Though any number of great minds of the past had a hand in building this branch of mathematics, you hear about some more than others. One of the most famous of these is Pythagoras. He was a philosopher, teacher and gifted mathematician, and he’s responsible for one of the most important rules about right triangles you’ll use in the world of geometry: the Pythagorean Theorem.
Pythagoras theorem goes like this: “The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.” When you’re using it to find your hypotenuse, it’ll be written:
a2 + b2 = c2
A right triangle always has one angle measuring 90 degrees. The hypotenuse, or the longest side, will be the one directly across from the right angle. When you’re using the Pythagoras theorem, it’ll always be your “c” side. Which one ends up being “a” or “b” really doesn’t matter one way or the other, but the side across from the right angles must be “c”; otherwise, you’re setting yourself up for a big fall.
All that being said, let’s get started with a basic example of finding the length of the hypotenuse of a right triangle.
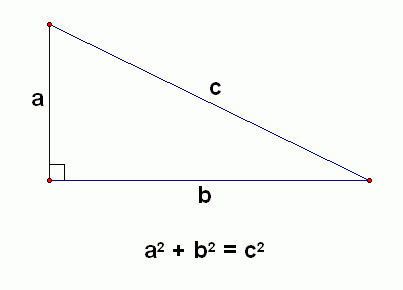
Say the length of side “a” in our example here is 12, and the length of side “b” is 8. Our job is to find the length of side “c”, so our problem will start off looking like this:
122 + 82 = c2
We have to square sides “a” and “b”, or multiply them by themselves, to get to our next step in the equation, bringing us to:
144 + 64 = c2
From there, we simply add the squares of “a” and “b” together to get closer to our mystery hypotenuse length.
208 = c2, or c2 = 208
Since 208 is actually the square of our hypotenuse, we’re not quite finished just yet. We have to find the square root of 208, which means finding the number you’d multiply by itself to get 208. If you have a scientific calculator at your fingertips, you could type in 208, hit the button that looks like an upward arrow (^), and type in .5. Alternately, you could hit the “2nd” button followed by the “x2”. Then, type in 208 and press the “enter/=” key.
If you’re ciphering without technology to back you up, it’s just a matter of finding two numbers that come close to 208 when squared, one slightly below and one just above it. As it happens, 142 is 195 and 152 is 225, so:
c ≈ 14.5 by mental math, or c ≈ 14.4 according to the calculator.
You can also use the Pythagoras theorem to find the length of side “a” or “b” if you already know the length of the hypotenuse. Things just need to be rearranged a bit. Here’s another example:

Say we already know the length of the hypotenuse is 12, and the length of “b” is 9. Start off by writing the Pythagorean theorem equation just as you normally would, inserting the numbers we already have:
a2 + 92 = 122
This would then become:
a2 + 81 = 144
Since we have to balance out the equation to get “a” all by itself, we simply subtract 81 from both sides:
a2 + 81 – 81 = 144 – 81
a2 = 63
a ≈ 7.9
Pythagoras is said to have refused to allow his concepts to be written down, but his students passed along his teachings to others. Eventually, this theorem went public and gave us the power to find the length of any side of a right triangle as long as we have an idea of what the other two might be.