Squares are very simple creatures. They’re two-dimensional shapes with four equal sides and four right angles formed where those sides come together. You’ll never need to worry about dealing with confusing formulas to find any missing angles in a square because all four are, without question, going to be 90 degrees. No complicated equations are necessary for finding the lengths of unlabeled sides; as long as you know the length of one side, the other three are going to be identical.
Finding the Area of a Square
When you’re figuring out the area of a square, you’re measuring the size of its surface. You can think of it as finding how many square units make up the entire surface. For squares, the formula for determining area is A = s2, or A = side x side. Have a look at an example.
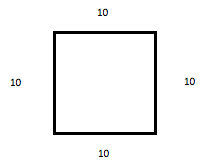
Here, your sides each measure 10, so you’d find the area like this:
A = s2
A = 102
A = 10 x 10
A = 100
Since all four angles of a square measure 90 degrees, squares are also rectangles. Having parallel opposite sides makes squares parallelograms as well. Because all the sides of a square have the same length, squares are also rhombuses. Not all parallelograms, rectangles or rhombuses are squares, but all squares fall into all those categories.
With all that in mind, you can also use other formulas for figuring out the area of a square. Let’s start with the formula for finding the area of a rectangle (A = l x w) using 14 as the measurement of our sides.
A = l x w
A = 14 x 14
A = 196
When it comes to parallelograms, the formula you’d use is A = b x h. With parallelograms, even though the sides are parallel, the angles aren’t necessarily 90 degrees. This means you’d need to have a line drawn from one angle of the shape to form a 90 degree angle with its base to find its height. Of course, since you’re dealing with a square, the perpendicular junction of your side and base already serve the purpose perfectly. We’ll say the height and base are 39.43 this time around.
A = b x h
A = 39.43 x 39.43
A = 1,554.72
If you find yourself in a position where you haven’t been given the length of a side of a square but you happen to know the distance between opposite corners, you can still find the area. The length from one corner to its opposite is known as the diagonal. The formula for finding the area of a rhombus, A = (p x q) / 2, comes into play here.
“P” and “q” simply stand for the two diagonals involved. With a square, they’re going to be the same, so as long as you have the length of one diagonal, you’re in great shape. Let’s use 9.72 for this example.
A = (p x q) / 2
A = (9.72 x 9.72) / 2
A = 94.48 / 2
A= 47.24
Some helpful resources for further explanations of and practice with any of these formulas are:
- Math Open Reference
- Math is Fun
- Math Goodies
In a nutshell, as long as you have the length of one side of a square, you can easily figure out its area. Whether you’re looking at it from an s2, l x w or b x h point of view, the process is very much the same. In the event your side lengths have been left out of the equation, a diagonal makes a nice stand-in.