The MRB constant is the upper limit point of the sequence of partial sums defined by:
[tex]\displaystyle S(x) = \sum_{n=1}^{x}{(-1)^n n^\frac{1}{n}}[/tex].
The goal of this article is to show that the MRB constant is geometrically quantifiable. To “measure” the MRB constant, we will consider a set, sequence and alternating series of the nth roots of n. Then we will compare the length of the edges of a special set of hypercubes or n-cubes which have a content of n. (The two words hypercubes and n-cubes will be used synonymously.)
Finally we will look at the value of the MRB constant as a representation of that comparison, of the length of the edges of a special set of hypercubes, in units of dimension 1/ (units of dimension 2 times units of dimension 3 times units of dimension 4 times etc.). For an arbitrary example we will use units of length/ (time*mass* density*…).
A Countable Infinite Set
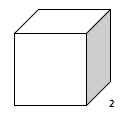
Consider, r, the set of roots of positive integers of the form r = n^(1/n). Of course the elements of this set are of the form x^(1/y). However what is not obvious is the geometric interpretation of x^(1/y). At least as far as natural number valued (x and y)>0 are concerned, x represents the content of an n-cube and y represents its dimension. That is a geometric interpretation of x^(1/y) as far as natural number valued (x and y)>0 are concerned. For instance we take a cube of any given volume and find the length of one of its sides. Let’s suppose the volume was 8 units^3. What would be the length of one of its sides? We might easily deduce that the length is 2. To confirm this answer we simply construct a cube of 2 linear units in length as in Diagram 1 and find its volume.
The volume in units3 of the cube in Diagram 1 is indeed 2*2*2 = 8.
Now we look at the previous sentence with x^(1/y) in mind. 8^(1/3) = 2 implies the volume of the cube in Diagram 1 raised to the power of the reciprocal of its dimension equals the length of one of its sides. That is a geometric interpretation of x^(1/y) as far as natural number valued x and y > 0 are concerned.
Open Question
What is the geometric interpretation of x^(1/y) for all real values of x,y > 0?
Sequence and Alternating Series
Now we will consider the sequence of roots of positive integers of the form r = {n^(1/n)} = {1^(1/1), 2^(1/2), 3^(1/3), …}. Then we will add the elements of r in the alternating series
[tex]\displaystyle L = \sum_{n=1}^{\infty}{(-1)^n r(n)} = \sum_{n=1}^{\infty}{(-1)^n n^\frac{1}{n}}.[/tex]
Concerning the partial sums of L, we remember
[tex]\displaystyle S(x)= \sum_{n=1}^{x}{(-1)^n n^\frac{1}{n}}[/tex]
and we find, S(x) is divergent as x goes to infinity. However S(2x) and S(2x+1) are both convergent as x goes to infinity and the difference between S(2x) and S(2x+1) also converges.
Special Hypercubes
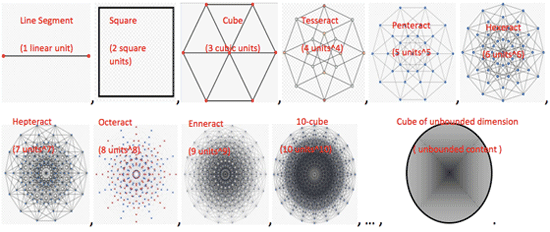
In geometric terms: As in Diagram 2, we give each n-cube a content equal to its dimension1,
so that we have a line segment of 1 linear unit, a square of 2 square units, and so forth.
The last cube in the diagram may be just an invention of the imagination because who has ever heard of a hypercube of unbounded dimension with unbounded content? Furthermore, there seems to be a paradox invoked when taking n-cubes as n->∞. While n is still a number the content of the n-cube or hypercube is defined in the specific unit of choice, whether the unit is inches, meters or what not and the resulting length of an individual edge is also defined in the same unit and is computed as shown above. “The [content] of the [n-]cube raised to the power of the reciprocal of its dimension equals the length of one of its [edges].”
However, when we arrived at the hypercube of unbounded dimension where n is no longer a number, the assigned “unbounded content” could be meant to be in units of feet, let’s say; while the resulting length of an individual edge is [tex]\displaystyle \lim_{u \to \infty}{u^\frac{1}{u}} = 1[/tex] which could be in feet or any other unit of length because there are the same amount of inches or meters or any other unit of length in infinity feet as there are feet. To avoid the resulting ambiguity we will look at the sequence of roots of positive integers of the form r = {n^(1/n)} = {1^(1/1), 2^(1/2), 3^(1/3), …} as being analogous to the clopen interval [1, ∞).
A Sum of the Series
Above it is mentioned, “Add the elements of r in the alternating series
[tex]\displaystyle L = \sum_{n=1}^{\infty}{(-1)^n r(n)} = \sum_{n=1}^{\infty}{(-1)^n n^\frac{1}{n}}.[/tex]”
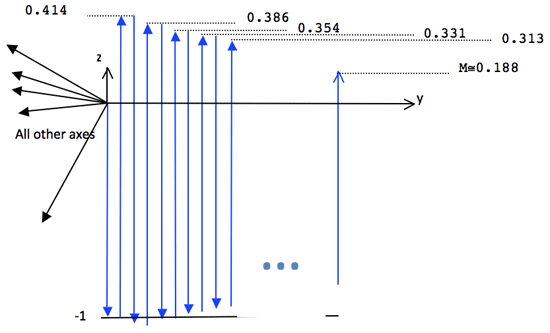
To show that geometrically we do the following: as in Diagram 3, on the y,z-plane line up an edge of each n-cube or hypercube. The numeric values displayed in the diagram are the partial sums of S(x) = S(2u) where u is a positive integer:
[tex]\displaystyle S(x)=\sum_{n=1}^{x}{(-1)^n n^\frac{1}{n}}.[/tex]
Notice a directed line segment is moved from the origin down the (z or y=0)-axis. Then at the y=1δ axis another one is moved up 2^(1/2) units. Then at the y=2δ axis yet another one is moved down 3^(1/3) units, etc. It does not matter whether δ is one or any other real value; there still are an infinite number of y-valued axes with matching directed line segments.
This is hard to understand; but we may say metaphorically that Diagram 3 is the path along the units of a particle moved 1 inch down in 2^(1/2) seconds, losing 3^(1/3) units of mass with density that increases 4^(1/4) units etc. The resulting position and condition of the particle is represented by
[tex]\displaystyle M = \lim_{u \to \infty}{\left ( \sum_{n=1}^{2u}{(-1)^n n^\frac{1}{n}} \right )}.[/tex]
The MRB Constant
As the dimension and the content of a hypercube, both go to infinity we have the following: First, in Diagram 2 the difference between the length of an edge of the hypercube with content 2n+1, and an edge of the hypercube with content 2n, goes to the constant value,
[tex]\displaystyle \lim_{n \to \infty}{\left ( (2n +1)^\frac{1}{2n+1}-(2n)^\frac{1}{2n} \right )} = 0.[/tex]
So as n goes to infinity, the length of an edge of the hypercube with content 2n and an edge of the hypercube with content 2n+1 become closer to being the same. Second, in Diagram 3 an edge of each n-cube is arranged on y-valued axes in such a way that
[tex]\displaystyle \sum_{n=0}^{\infty}{\left ( (2n +1)^\frac{1}{2n+1}-(2n)^\frac{1}{2n} \right )} = \lim_{u \to \infty}{\left ( \sum_{n=1}^{2u}{(-1)^n n^\frac{1}{n}} \right )}.[/tex]
M is the MRB constant2.
A numerical approximation of M can be computed by the following summation
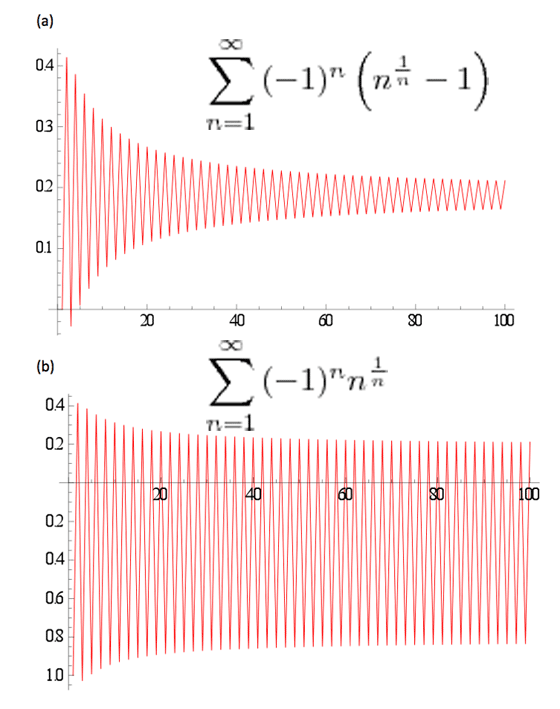
[tex]\displaystyle \sum_{n=1}^{\infty}{(-1)^n \left (n^\frac{1}{n}-1 \right )}[/tex],
which sum converges3 (see Diagram 4), while
[tex]\displaystyle \sum_{n=1}^{\infty}{(-1)^n n^\frac{1}{n}}[/tex]
diverges4, as mentioned above.
One should use acceleration methods when computing a numerical approximation of the MRB constant because it can be shown that one must sum a number in the order of 10^(n+1) iterations of (-1)^n*(n^(1/n)-1) to get n accurate digits of the MRB Constant. However, using a convergence acceleration of alternating series algorithm of Cohen-Villegas-Zagier one can compute the first 60 digits in only 100 iterations5.
In Diagram 4a both the lim sup6 and the lim inf converge upon the MRB constant, while in 4b only the lim sup converges upon it with the lim inf converging upon MRB constant-1. The MRB constant is Sloane’s On-Line Encyclopedia of Integer Sequences id:A0370777. More information, including a brief but documented history, can be found in Wikipedia8.
Summary
In retrospect, the geometry used here, particularly in diagram3, is transdimensional and thus we find it hard to understand through the previous experiences of our senses. (To examine its geometry we used edges from hypercubes of many dimensions.) However, considering the various temporal-spatial dimensions that affect our universe as proposed in some theories9 is there some significance to the MRB constant in our daily lives? Nevertheless, we have seen that the value of the MRB constant is geometrically quantifiable; it is the lim sup of the sequence that represents a particle traveling along a directed line segment that is moved 1 unit from the origin down the z-axis; at the y=1δ moved up 2^(1/2) units’ at the y=2δ axis moved down 3^(1/3) units etc. Whether the units are theoretical (as in units of length/ (time*mass* density*…)) or proposed temporal-spatial dimensions, the resulting z value of the particle’s position and condition
[tex]\displaystyle M = \lim_{u \to \infty}{\left ( \sum_{n=1}^{2u}{(-1)^n n^\frac{1}{n}} \right )}.[/tex]
This article is released under the Creative Commons Attribution-Share Alike 3.0 Unported license.
About the author
Marvin Ray Burns has indulged in math research as a hobby since 1994. Having had only one college course, most of his discoveries were simply learning the basics of math. He has cataloged many of his early investigations at https://math2.org/mmb/search?query=Marvin. One of his ideas has served some purpose in the math world; that is the MRB constant. Since the discovery of the MRB constant, at least one major mathematics software company has found that it was useful to fix problems found while computing the MRB constant. Another major company changed the functionality of its sum function in such a way as to be able to compute the digits of the MRB constant shortly after its discovery. Mr. Burns has submitted a few integer sequences based on his explorations of the MRB constant; see https://www.research.att.com/~njas/sequences/?q=A037077. A siding applicator by profession, he presently takes various undergraduate courses at IUPUI in the hopes of obtaining a degree in pure math.
References
[1] https://www23.wolframalpha.com/input/?i=n-cube
[2] S. R. Finch, Mathematical Constants, Cambridge, 2003, p. 450.
[3] https://mathworld.wolfram.com/MRBConstant.html
[4] https://mathworld.wolfram.com/notebooks/Constants/MRBConstant.nb
[5] https://arxiv.org/abs/0912.3844
[6] https://en.wikipedia.org/wiki/Upper_limit
[7] https://oeis.org/A037077
[8] https://en.wikipedia.org/wiki/MRB_constant
[9] https://arxiv.org/abs/hep-ph/9803466
Here are some Octave scripts to generate the plots in Diagram 4 in the article: https://gist.github.com/712629
Octave is a free MATLAB compatible numerical programming environment available under the GNU General Public LIcense. Binaries are available for MS Windows, Unix, and Macintosh platforms: https://www.gnu.org/software/octave/
John
John,
I downloaded A precompiled windows version of octive (octave-3.2.4.exe), copied and pasted the entire code from https://gist.github.com/712629 into a command prompt. It ran and gave me two windows for plots with a number at the bottom of each, (probably the “maximum number “i.e. infinity), but no plots.
I’m using Windows 7 ultimate 64 Bit.
As I understand, you are looking for a way to determine a constant (K) as an exclusive parameter to determine a quantifiable value for non linear integral calculus that we can call unidimensonnal or dimension1. Personnally, I have still made calculus for a circular domain of integration and I define this integral calculus from a standard integral as :
n = infinity
S(x) = linInteg (360degree)
n = 0
// n is a reference point on a circular curve and x is the curve itself (x = 360degree)
I will let you make standard applicable to this type of simple degree 1 integral. If you succeed in resolving it, you will discover that integral (sums)calculus cannot be defined as a simple pure constant (K), and from that point, it is a more valuable way to create your own calculus formula depending to situation requirement. As a path to make you such type of a degree higher calculus, let me introduce you a formula that can be used :
n = infinity
linInteg(y*2)
n = 0
S(x*(y)) = linIntg (define domain)
n = infinity
linInteg(y*1)
n = 0
where y = number of related dimension and n = a referenced point *on* that dimension
It seems to be a hard calculus, but maths are so easy when we take time to understand that 1 + 1 = 2 !!!
Good luck!!!
error on second integral calculus formula. You should read :
n = infinity
linInteg(domain of dimension2)
n = 0
S(x*(y)) = linInteg (domain of *entity*)
n = infinity
linInteg(domain of dimension1)
n = 0
Hello Marvin,
Take the functions
mrb, mrb_sequence, and mrb_simple
Put each function in a *.m file of the same name:
mrb.m, mrb_sequence.m, and mrb_simple.m in the working directory (folder) of Octave.
Then, if you do help mrb, help mrb_sequence, and help mrb_simple.m, you should see the help comments in each function file. You should also be able to invoke each function from the Octave command prompt, e.g.
octave-3.2.3:2> mrb(10)
ans = 0.31323
octave-3.2.3:3> mrb_sequence(10)
ans =
0.00000 0.41421 -0.02804 0.38618 0.00645 0.35445 0.03398 0.33082 0.05431 0.31323
octave-3.2.3:4> mrb_simple(10)
ans = 0.31323
Then, put the main script in a file mrb_plots.m or run directly from the Octave command prompt. This should produce the actual plots in the figure windows.
Sincerely,
John
I got one of the plots to appear. But I got the following error.
error: `mrb_simple’ undefined near line 6 column 18
Hello Marvin,
I downloaded the code to my Windows XP computer with Octave 3.2.4 and copied the code for the function mrb_simple into mrb_simple.m in the bin folder of Octave.
It appears to work on my computer. Here is the output from the Octave command prompt:
GNU Octave, version 3.2.4
Copyright (C) 2009 John W. Eaton and others.
This is free software; see the source code for copying conditions.
There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. For details, type `warranty’.
Octave was configured for “i686-pc-mingw32”.
Additional information about Octave is available at https://www.octave.org.
Please contribute if you find this software useful.
For more information, visit https://www.octave.org/help-wanted.html
Report bugs to (but first, please read
https://www.octave.org/bugs.html to learn how to write a helpful report).
For information about changes from previous versions, type `news’.
octave-3.2.4.exe:1> pwd
ans = D:\Octave\3.2.4_gcc-4.4.0\bin
octave-3.2.4.exe:2> help mrb_simple
`mrb_simple’ is a function from the file D:\Octave\3.2.4_gcc-4.4.0\bin\mrb_simple.m
to help compute the MRB constant
[val] = mrb_simple(n)
n is number of elements in sum
sum_i_n (-1)^i (i^(1/i) )
Author: John F. McGowan, Ph.D.
Additional help for built-in functions and operators is
available in the on-line version of the manual. Use the command
`doc ‘ to search the manual index.
Help and information about Octave is also available on the WWW
at https://www.octave.org and via the help@octave.org
mailing list.
octave-3.2.4.exe:3> mrb_simple(10)
ans = 0.31323
octave-3.2.4.exe:4>
I am wondering if there could be a typo. Line six (6) of the function definition is a comment line beginning with a percent (%) sign, the Octave/Matlab comment symbol. I have found the Octave error messages can be cryptic and unhelpful. It is a useful tool and highly compatible with Matlab, but the error messages could be improved.
Sincerely,
John
thanks for inventing mathematical formulae