Z-table: Left and Right Z-score Tables

Z-score tables, also known as standard normal tables or Z-tables, provide a way to find the probability of a particular Z-score occurring within a normal distribution. There are two types of Z-score tables: left-tailed (negative Z-scores) and right-tailed (positive Z-scores). These tables help in determining how unusual or typical a particular score is within a dataset.

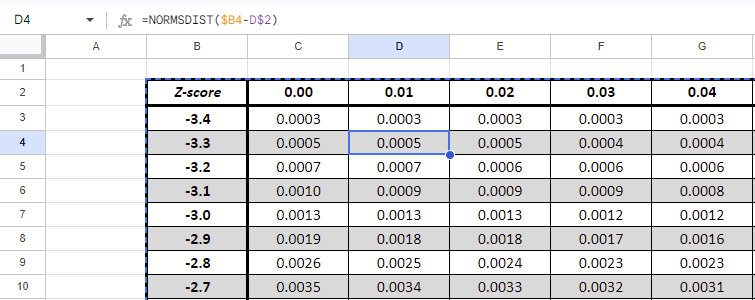
Reading the Left Z-score Table (Negative)

The left Z-score table typically lists Z-scores on the leftmost column, representing data points below the mean. The body of the table shows the probability of a score falling at or below a given Z-score. For instance, a Z-score of -1.96 corresponds to a probability of approximately 0.025. This means there’s a 2.5% chance of a score falling below this Z-score in a standard normal distribution.

Reading the Right Z-score Table (Positive)

Conversely, the right Z-score table deals with positive Z-scores, which are scores above the mean. Reading this table involves understanding the probability of a score falling at or above a particular Z-score. For example, a Z-score of 1.96 in a right-tailed table also indicates a 2.5% chance, but this time it’s the likelihood of a score falling above this value.

Practical Examples and Applications

In a college entrance exam with a mean score of 500 and a standard deviation of 100, what is the probability of a student scoring less than 450?

Solution: To find this, we first calculate the Z-score.

The formula for Z-score is \( Z = \frac { X – mean}{standard_deviation} \)

For our example Z-score = \( \frac {(450−500)}{100} = -0.5\)

A Z-score of -0.5 indicates that the score of 450 is half a standard deviation below the mean. Now, using the left Z-score table, we look up the probability corresponding to a Z-score of -0.5. In the table, this value is 0.3085. This means there’s a 30.85% chance of a student scoring below 450 on this exam.

Note: Since a Z-score of -0.5 is relatively close to the mean it suggests that scoring below 450 is not highly unusual in this distribution.

Limitations and Considerations

While Z-score tables are incredibly useful, they have limitations. They are only accurate for normally distributed data. In datasets with significant skew or kurtosis, Z-scores might not provide the correct insights. That’s why it’s crucial to understand the context and nature of the data when applying Z-scores.

Below we explain why context matters, along with some “on the contrary” examples:

a) Normal Distribution Assumption: Z-scores are based on the assumption that the data follows a normal distribution. If the data is heavily skewed or has a significant departure from normality, using Z-scores might lead to misleading interpretations.

• Deviant Scenario: In a dataset representing annual incomes in a region with a large income disparity, the distribution might be right-skewed with a few very high incomes. Using Z-scores here could suggest that moderately high incomes are more ‘unusual’ than they actually are, due to the influence of the extremely high incomes.

b) Outliers Impact: Z-scores are sensitive to outliers. In datasets with extreme values, the mean and standard deviation (which are used to calculate Z-scores) can be heavily influenced by these outliers, leading to distorted Z-scores.

• Deviant Scenario: In a small class’s test scores, if one student scores exceptionally high or low, it can skew the average and standard deviation, thus affecting the Z-scores of all other students. A score that would normally be considered average might appear as an outlier when it is actually not.

c) Scale and Units of Measurement: The meaning and implications of a Z-score can vary depending on the scale and units of measurement in the dataset. This necessitates understanding the data’s context to interpret Z-scores correctly.

• Deviant Scenario: In psychological testing, a Z-score might indicate a clinically significant deviation from the norm. However, the same Z-score in a different context, like height measurements in a population, might be perfectly normal and not indicate any unusual characteristic.

d) Misinterpretation of Probabilities: Z-scores correspond to probabilities in a normal distribution. Misinterpreting these probabilities can lead to incorrect conclusions, especially in non-normal distributions.

• Deviant Scenario: In a distribution of a rare event, like major natural disasters, using Z-scores might suggest a higher probability of extreme values than what is realistically the case, as rare events do not typically follow a normal distribution.

Z-table in HTML Format

Below you can see the HTML versions of the left Z-table and the right Z-table, which allows copy and pasting.

Left Z-table

Z-score	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
-3.4	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003	0.0003	0.0002
-3.3	0.0005	0.0005	0.0005	0.0004	0.0004	0.0004	0.0004	0.0004	0.0004	0.0003
-3.2	0.0007	0.0007	0.0006	0.0006	0.0006	0.0006	0.0006	0.0005	0.0005	0.0005
-3.1	0.0010	0.0009	0.0009	0.0009	0.0008	0.0008	0.0008	0.0008	0.0007	0.0007
-3.0	0.0013	0.0013	0.0013	0.0012	0.0012	0.0011	0.0011	0.0011	0.0010	0.0010
-2.9	0.0019	0.0018	0.0018	0.0017	0.0016	0.0016	0.0015	0.0015	0.0014	0.0014
-2.8	0.0026	0.0025	0.0024	0.0023	0.0023	0.0022	0.0021	0.0021	0.0020	0.0019
-2.7	0.0035	0.0034	0.0033	0.0032	0.0031	0.0030	0.0029	0.0028	0.0027	0.0026
-2.6	0.0047	0.0045	0.0044	0.0043	0.0041	0.0040	0.0039	0.0038	0.0037	0.0036
-2.5	0.0062	0.0060	0.0059	0.0057	0.0055	0.0054	0.0052	0.0051	0.0049	0.0048
-2.4	0.0082	0.0080	0.0078	0.0075	0.0073	0.0071	0.0069	0.0068	0.0066	0.0064
-2.3	0.0107	0.0104	0.0102	0.0099	0.0096	0.0094	0.0091	0.0089	0.0087	0.0084
-2.2	0.0139	0.0136	0.0132	0.0129	0.0125	0.0122	0.0119	0.0116	0.0113	0.0110
-2.1	0.0179	0.0174	0.0170	0.0166	0.0162	0.0158	0.0154	0.0150	0.0146	0.0143
-2.0	0.0228	0.0222	0.0217	0.0212	0.0207	0.0202	0.0197	0.0192	0.0188	0.0183
-1.9	0.0287	0.0281	0.0274	0.0268	0.0262	0.0256	0.0250	0.0244	0.0239	0.0233
-1.8	0.0359	0.0351	0.0344	0.0336	0.0329	0.0322	0.0314	0.0307	0.0301	0.0294
-1.7	0.0446	0.0436	0.0427	0.0418	0.0409	0.0401	0.0392	0.0384	0.0375	0.0367
-1.6	0.0548	0.0537	0.0526	0.0516	0.0505	0.0495	0.0485	0.0475	0.0465	0.0455
-1.5	0.0668	0.0655	0.0643	0.0630	0.0618	0.0606	0.0594	0.0582	0.0571	0.0559
-1.4	0.0808	0.0793	0.0778	0.0764	0.0749	0.0735	0.0721	0.0708	0.0694	0.0681
-1.3	0.0968	0.0951	0.0934	0.0918	0.0901	0.0885	0.0869	0.0853	0.0838	0.0823
-1.2	0.1151	0.1131	0.1112	0.1093	0.1075	0.1056	0.1038	0.1020	0.1003	0.0985
-1.1	0.1357	0.1335	0.1314	0.1292	0.1271	0.1251	0.1230	0.1210	0.1190	0.1170
-1.0	0.1587	0.1562	0.1539	0.1515	0.1492	0.1469	0.1446	0.1423	0.1401	0.1379
-0.9	0.1841	0.1814	0.1788	0.1762	0.1736	0.1711	0.1685	0.1660	0.1635	0.1611
-0.8	0.2119	0.2090	0.2061	0.2033	0.2005	0.1977	0.1949	0.1922	0.1894	0.1867
-0.7	0.2420	0.2389	0.2358	0.2327	0.2296	0.2266	0.2236	0.2206	0.2177	0.2148
-0.6	0.2743	0.2709	0.2676	0.2643	0.2611	0.2578	0.2546	0.2514	0.2483	0.2451
-0.5	0.3085	0.3050	0.3015	0.2981	0.2946	0.2912	0.2877	0.2843	0.2810	0.2776
-0.4	0.3446	0.3409	0.3372	0.3336	0.3300	0.3264	0.3228	0.3192	0.3156	0.3121
-0.3	0.3821	0.3783	0.3745	0.3707	0.3669	0.3632	0.3594	0.3557	0.3520	0.3483
-0.2	0.4207	0.4168	0.4129	0.4090	0.4052	0.4013	0.3974	0.3936	0.3897	0.3859
-0.1	0.4602	0.4562	0.4522	0.4483	0.4443	0.4404	0.4364	0.4325	0.4286	0.4247
-0.0	0.5000	0.4960	0.4920	0.4880	0.4840	0.4801	0.4761	0.4721	0.4681	0.4641

Right Z-table

Z-score	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.5000	0.5040	0.5080	0.5120	0.5160	0.5199	0.5239	0.5279	0.5319	0.5359
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	0.5596	0.5636	0.5675	0.5714	0.5753
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	0.5987	0.6026	0.6064	0.6103	0.6141
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	0.6368	0.6406	0.6443	0.6480	0.6517
0.4	0.6554	0.6591	0.6628	0.6664	0.6700	0.6736	0.6772	0.6808	0.6844	0.6879
0.5	0.6915	0.6950	0.6985	0.7019	0.7054	0.7088	0.7123	0.7157	0.7190	0.7224
0.6	0.7257	0.7291	0.7324	0.7357	0.7389	0.7422	0.7454	0.7486	0.7517	0.7549
0.7	0.7580	0.7611	0.7642	0.7673	0.7704	0.7734	0.7764	0.7794	0.7823	0.7852
0.8	0.7881	0.7910	0.7939	0.7967	0.7995	0.8023	0.8051	0.8078	0.8106	0.8133
0.9	0.8159	0.8186	0.8212	0.8238	0.8264	0.8289	0.8315	0.8340	0.8365	0.8389
1.0	0.8413	0.8438	0.8461	0.8485	0.8508	0.8531	0.8554	0.8577	0.8599	0.8621
1.1	0.8643	0.8665	0.8686	0.8708	0.8729	0.8749	0.8770	0.8790	0.8810	0.8830
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944	0.8962	0.8980	0.8997	0.9015
1.3	0.9032	0.9049	0.9066	0.9082	0.9099	0.9115	0.9131	0.9147	0.9162	0.9177
1.4	0.9192	0.9207	0.9222	0.9236	0.9251	0.9265	0.9279	0.9292	0.9306	0.9319
1.5	0.9332	0.9345	0.9357	0.9370	0.9382	0.9394	0.9406	0.9418	0.9429	0.9441
1.6	0.9452	0.9463	0.9474	0.9484	0.9495	0.9505	0.9515	0.9525	0.9535	0.9545
1.7	0.9554	0.9564	0.9573	0.9582	0.9591	0.9599	0.9608	0.9616	0.9625	0.9633
1.8	0.9641	0.9649	0.9656	0.9664	0.9671	0.9678	0.9686	0.9693	0.9699	0.9706
1.9	0.9713	0.9719	0.9726	0.9732	0.9738	0.9744	0.9750	0.9756	0.9761	0.9767
2.0	0.9772	0.9778	0.9783	0.9788	0.9793	0.9798	0.9803	0.9808	0.9812	0.9817
2.1	0.9821	0.9826	0.9830	0.9834	0.9838	0.9842	0.9846	0.9850	0.9854	0.9857
2.2	0.9861	0.9864	0.9868	0.9871	0.9875	0.9878	0.9881	0.9884	0.9887	0.9890
2.3	0.9893	0.9896	0.9898	0.9901	0.9904	0.9906	0.9909	0.9911	0.9913	0.9916
2.4	0.9918	0.9920	0.9922	0.9925	0.9927	0.9929	0.9931	0.9932	0.9934	0.9936
2.5	0.9938	0.9940	0.9941	0.9943	0.9945	0.9946	0.9948	0.9949	0.9951	0.9952
2.6	0.9953	0.9955	0.9956	0.9957	0.9959	0.9960	0.9961	0.9962	0.9963	0.9964
2.7	0.9965	0.9966	0.9967	0.9968	0.9969	0.9970	0.9971	0.9972	0.9973	0.9974
2.8	0.9974	0.9975	0.9976	0.9977	0.9977	0.9978	0.9979	0.9979	0.9980	0.9981
2.9	0.9981	0.9982	0.9982	0.9983	0.9984	0.9984	0.9985	0.9985	0.9986	0.9986
3.0	0.9987	0.9987	0.9987	0.9988	0.9988	0.9989	0.9989	0.9989	0.9990	0.9990
3.1	0.9990	0.9991	0.9991	0.9991	0.9992	0.9992	0.9992	0.9992	0.9993	0.9993
3.2	0.9993	0.9993	0.9994	0.9994	0.9994	0.9994	0.9994	0.9995	0.9995	0.9995
3.3	0.9995	0.9995	0.9995	0.9996	0.9996	0.9996	0.9996	0.9996	0.9996	0.9997
3.4	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9997	0.9998

Related: Check out our Z-score calculator for easier computations.

How do I make my own Z-score tables in Google Sheets?

Start by creating the header column: 0.00 to 0.09 (increments of 0.01). The create the vertical ones 0.0 to whatever you choose (increments of 0.1).

Then use the NORMDIST() function and sum up (for the right Z-table) the two cells you need. In our case D4 is “=NORMDIST($B4 + D$2)”. Blocking the B column and the $2 row in the formula allos for dragging it to the whole table and generate the needed Z-score values.

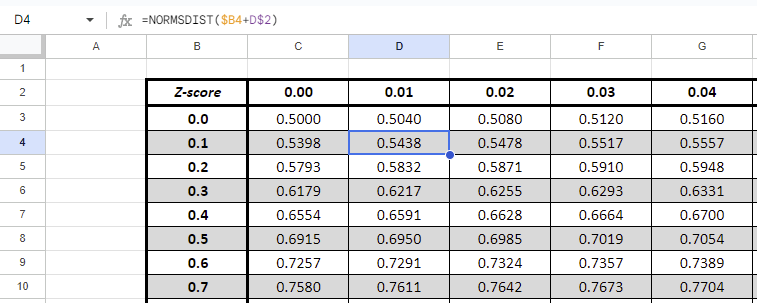
You do similarly with the left Z-table except that you need to substract instead of summing the two cells.