The Absolute Error is the quantifiable difference between a measured value and its actual value. It is obtained by taking the absolute value between the predicted or observed value and the true value. The absolute error is not just a reflection of the measurement’s deviation from the true value, it is a direct indicator of the reliability and precision of the measurement process itself.

Absolute error and Mean Absolute Error explained

How to Calculate the Absolute Error

The formula for absolute error is:

\[Absolute Error = |Observed Value – Actual Value| \]

or

\[ \Delta x = |x_i – x| \]

where:

  • \( \Delta x \) is the absolute error,
  • \( x_i \) is the actual value,
  • \( x \) is the measured value.

The use of the absolute value ensures that the error magnitude is accurately reflected, regardless of its direction. As an example, let’s say the actual temperature for a particular day is 82°F, and the predicted temperature generated by the model is 86°F. The absolute error would be:

\[ | 82- 86 | = 4\]

What Is Absolute Accuracy Error?

Absolute Error is also referred to as Absolute Accuracy Error. This term represents the same concept with a different nomenclature: \( E = x_e – x_t \). Here, \( x_e \) stands for x_experimental and is the measurement taken, and \( x_t \) is the x_true, the actual, accurate value​​. This alternative terminology emphasizes the role of absolute error in evaluating the accuracy of experimental results.

The Mean Absolute Error (MAE)

The mean absolute error (MAE) represents the average of all absolute errors in a set of measurements​​​​. MAE is a useful metric for evaluating the accuracy of predictions or forecasts, particularly in cases where the data has 1-dimensional characteristics. It provides a clear indication of the average magnitude of error and offers a straightforward way to compare the performance of different models or data categories.

The mean absolute error can then be calculated as the average of all absolute errors, using the formula:

\[ MAE = \frac{1}{n} \sum_{i=1}^{n} |x_i – x| \]

where \( n \) represents the number of errors (or data points).

Application in Different Fields, Comparison with Other Error Measures

MAE finds applications in various domains, such as time series analysis, where it serves as a common measure of forecast error, and in remote sensing, where it helps in understanding both quantity and allocation disagreements​​​​.

While similar to other error metrics like Mean Squared Error (MSE), MAE stands out for its simplicity and direct interpretability. Unlike MSE, which squares the differences, potentially exaggerating large errors, MAE provides a more balanced and linear view of the error magnitudes​​.

MAE Practical Examples

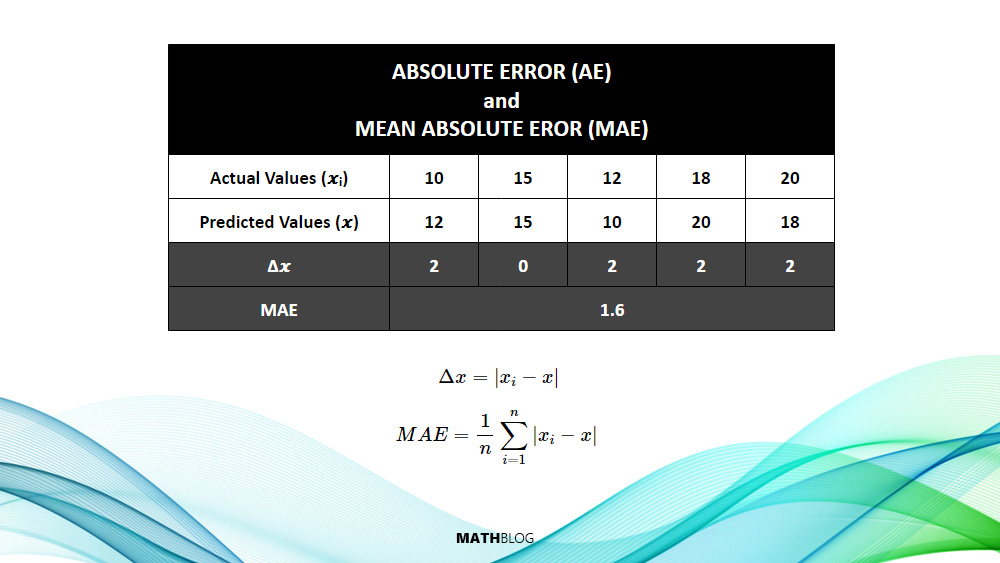
Consider a scenario involving multiple temperature measurements. The MAE in this case would be the average of the absolute differences between each recorded temperature and the true temperature, offering a clear picture of the overall accuracy of the measurements.

\[ \text{Actual Values: } [ 10, 15, 12, 18, 20 ] \] \[ \text{Predicted Values: } [ 12, 15, 10, 20, 18 ] \]

That means:

\[ i=1 … | 10 – 12 | = 2 \] \[ i=2 … | 15 – 15 | = 0 \] \[ i=3 … | 12 – 10 | = 2 \] \[ i=4 … | 18 – 20 | = 2 \] \[ i=5 … | 20 – 18 | = 2 \]

To calculate the Mean Absolute Error (MAE), you now sum up all the absolute errors (2 + 0 + 2 + 2 +2) and then divide by the number of observations (5).

\[ MAE = \frac{2 + 0 + 2 + 2 + 2 }{5} = \frac{8}{5} = 1.6 \]

The MAE in this case is 1.6. This value represents the average magnitude of the errors between the actual and predicted values, without considering their direction. In other words, on average, the predictions deviate from the actual values by 1.6 units.

This is a measure of the accuracy of the predictions: the lower the MAE, the more accurate the predictions. An MAE of 1.6 suggests that the predictions are fairly close to the actual values, with an average error of 1.6 units per prediction.