Imagine a rope that was just long enough to wrap tightly around the equator of a perfectly spherical earth. Now imagine that the length of that rope is increased by one meter and again wrapped around the earth, supported in a regular way, so as to form an annulus. Doing things in this way will form a certain gap between the earth and the extended rope. Now imagine that you repeat the process with a golf ball. How do the two gaps compare?
Most people who understand the problem correctly, will immediately assume that adding a single meter to the rope surrounding the huge spherical earth won’t create much of a gap, while adding a single meter to the rope around the golf ball, will create a large gap. In reality, the two gaps are identical. It’s counterintuitive, but it can be proven easily with elementary mathematics.
We know that:
[tex]C = 2 \pi r[/tex]
[tex]C + 1 = 2 \pi R[/tex]
Where C is the length of the rope around a given spherical object, C+1 is obviously the length of the longer (by one meter) rope, r is the radius of the object (e.g. the golf ball) and R the radius of the annulus. We can express the two equations above as such:
[tex]\displaystyle r = \frac{C}{2\pi}[/tex]
[tex]\displaystyle R = \frac{C+1}{2\pi}[/tex]
The width of the gap between the longer rope and the object that’s taken into consideration is R-r.
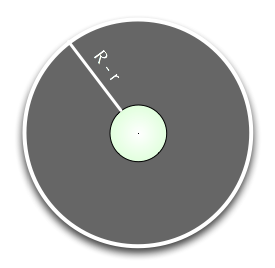
Therefore:
[tex]\displaystyle R – r = \frac{C+1}{2\pi} – \frac{C}{2\pi} = \frac{1}{2\pi} \approx 0.159[/tex]
The gap, as you can see, is constant at about 16 cm, and it doesn’t depend in any way on the size of the radius (r) of the object at hand. That means that the gap between the extended rope and the golf ball is the same as in the case of the spherical earth.
Quite a surprising result, isn’t it? This exact example opens up the book Impossible?: Surprising Solutions to Counterintuitive Conundrums which I received as a media copy in the mail. So far it’s been a very enjoyable and easy read, chocked full of surprising paradoxes and results which common sense would have you deem (practically) impossible or counterintuitive. To make things even nicer, the math involved is not overly advanced, and anyone who grasped high school level math, should have no problem following this engaging book.
The width of the gap might be constant, but the area wouldn’t be. It would be
pi*( (r+1)^2 – r^2) = pi*(2*r + 1), which clearly depends on r. Simply asking how the two gaps compare is a bit vague.
I think the real issue is that when you picture the problem, the gaps look different. A 16 cm wide gap doesn’t seem like much next to the radius of the Earth, but it seems like a lot next to the radius of a golf ball.
Yes Enginerd, the areas are obviously very different. The pardox is limited to the width of the gaps. 🙂
wait. this does sound impossible!
So, if the world had a 32 cm bigger diameter, you’d only need one more meter of rope to wrap it…
*thinks* actually that kind makes sense… because adding 1 meter to the circumference would increase the size by that ammount.
The thinking relies on making the 1 meter sound like the small measurement adjustment causing a huge 16cm change.
I’ve only just heard this paradox and likewise thought ‘that can’t be right’. But a pencil and paper proved me wrong.
In trying to convince my son I thought of a persuasive visualisation.
Assuming the rope runs through the poles, don’t add one meter to the rope, add 25cm four times – at both poles and at the equator (both sides) then the four ‘segments’ (arcs) can lift apart and away from the earth’s surface by about the amount the calculations show.
That visualisation persuaded him. And, finally, me.
that’s an amazing result. I can’t fault it but i also can’t really believe it is true. It just goes against any intuitive thought on the problem.