Simulating Cell Chemistry for Health and Medicine

Advances in mathematical and computer modeling of cell chemistry may lead to cures or effective treatments for major diseases such as cancer.

This article discusses using mathematics and computer models to simulate cell chemistry for health and medicine. First, it discusses why simulating cell chemistry may benefit readers. Second, it gives a brief technical introduction to simulating cell chemistry for a general audience using the free open-source program Smoldyn as an example of simulating cell chemistry. A simulation of the “Bathtub Mechanism,” a possible cure for cancer, is used as an example of simulating cell chemistry with Smoldyn. Third, it discusses the scope and difficulty level of simulating cell chemistry, something of particular relevance to policy makers and business leaders who may be interested in simulating cell chemistry to achieve practical benefits.

Why simulate cell chemistry?

There are many unsolved medical problems ranging from heart disease to stroke to the general aging process to cancer. In recent years, the pharmaceutical industry has encountered a shortage of new and effective drugs. Indeed in recent months, scientists at Bayer and Amgen have claimed to have been unable to reproduce large numbers of landmark cancer research results in high profile comments in the prestigious journal Nature. Since they have not identified the specific results and research papers that they could not reproduce, citing confidentiality requirements, it is difficult to evaluate such claims. The claims almost certainly reflect frustration with the current rate of progress in medical research, especially cancer.

Cancer is a prominent example of a disease or collection of diseases that may be defeated by detailed simulation of cell chemistry. Cancer is the second leading cause of death in the United States. If current trends continue and heart disease continues to decline, about one in three readers will die from cancer. About 500,000 people die from cancer in the United States each year.

About $200 billion has been spent on cancer research and development in the United States since 1971 when President Nixon declared the “War on Cancer”. Adjusting for inflation, this is about ten times the total budget for the wartime Manhattan Project which developed the atomic bomb and the first nuclear reactors. The current annual budget of the National Cancer Institute (NCI) is about $5 billion which is, again adjusting for inflation, about the annual budget of the Manhattan Project.

Although there have been some partial successes with rare cancers such as various types of leukemia, the results have been mostly disappointing. The age adjusted mortality rates today for cancer are about the same as during the 1950s. Since people are living longer today, the actual raw mortality rates have risen as cancer accounts for a larger and larger fraction of deaths among the aging population.

Cancer is now thought to be caused by the accumulation of around a dozen mutations among a collection of about two-hundred oncogenes, a fancy word for “cancer genes”, and tumor suppressor genes that have been identified since the 1970s. Many different combinations of mutations cause many different kinds of cancer. In fact, it is thought that there are many different kinds of each cancer: skin cancer, breast cancer, etc. Different skin cancers have been found to have different sets of mutated genes.

Even worse, cancer cells are thought to become genetically unstable and mutate rapidly, evolving immunity to anticancer drugs rapidly. Cells in the same tumor in the same patient have been found to contain different mutations of different genes. This presents considerable difficulties in developing an effective cure or treatment for cancer, at least if one focuses on the individual genes or the individual proteins produced by these genes.

What do the roughly two-hundred cancer genes and tumor suppressor genes actually do? They are thought to produce proteins that form complex control networks of chemical reactions that direct cell division, cell growth, cell death (cells are actually programmed to die under certain conditions), and cell differentiation. Cell differentiation refers to the process by which cells turn into specialized cells such as skin, muscle, nerves, brain, blood, and so forth in the right places in the body and at the right time.

In cancer, it is thought that the accumulation of several mutations of these genes leads to malfunctions of this control system. Cells divide when they should not; grow when they should not. Most importantly, cells such as skin cells in skin cancer, appear and grow in the vital organs such as the lungs and liver where they should not. It is generally thought that cancer cells migrate through the blood stream from the primary tumor to the vital organs where they take up residence and grow, slowly but surely killing the patient. This process is known as metastasis and is responsible for most cancer deaths. What we can be sure of is that cells that appear to be skin or other parts of the body are found growing in the vital organs when examined under a microscope.

There are many enigmas in cancer. For example, most cancers have far too many chromosomes, roughly cylindrical bundles of genetic material found in the nuclei of plant and animal cells. A normal healthy human being has forty-six chromosomes. A few people with unusual medical conditions have one or two extra chromosomes or one or two missing chromosomes. The wrong number of chromosomes is usually fatal and embryos with the wrong number usually perish. Cancer cells, however, often, perhaps always in some cancers, have many more chromosomes, about eighty or ninety. There are often extensive chromosomal rearrangements as well. This wrong number of chromosomes does not really fit well with the cancer gene theory which would seem to predict many cancers with the normal number of chromosomes.

Cancer cells apparently exhibit an unusual metabolism which led pioneer researcher Otto Warburg to propose an “oxygen deprivation” theory of cancer in the 1930’s. Other enigmas exist. These many enigmas are probably why there were many different theories of cancer prior to the rise of the cancer gene theory in the 1970s.

The state of cancer research may be like the ancient Indian folk tale of the blind men and the elephant. One blind man feels the elephant’s trunk and says “aha, it is like a snake”. The second blind man feels the elephant’s leg and says “aha, it is like a tree”, and so on. Each blind man deduces something different and seemingly contradictory to every other blind man.

Detailed simulation of cell chemistry may enable us to understand precisely the control networks implicated in cancer and what they do. More importantly, it may enable us to find ways to identify, selectively kill, or inhibit cancer cells independent of the confusing plethora of cancer genes and tumor suppressor genes and the seeming rapid mutation and evolution of the cancer cells.

A Brief Introduction to Simulating Cell Chemistry

The current theory of cell chemistry is that it proceeds through a combination of diffusion in which molecules spread randomly through the cellular medium, mostly water, and chemical reactions between different chemicals, mostly proteins. Diffusion is what happens when you add a single drop of colored dye to a glass of water. The dye spreads slowly, unevenly in the glass of water until it is uniformly distributed through the glass of water.

Imagine that one adds a drop of red dye to one side of a glass of water and a drop of blue dye to the other side of the glass of water. The drops of dye begin to spread until they meet. Imagine that the red and blue dye react to form a green dye. Green will begin to appear in the region where the clouds of red and blue dye overlap. In this simple case, over time, all of the dye will change to green dye uniformly distributed through the glass of water. This is a simple example of the reaction-diffusion process thought to dominate cell chemistry.

Cells are thought to contain not two chemicals diffusing and reacting, but thousands, further organized in compartments such as the cell nucleus and the organelles inside the cell. These thousands of chemicals are thought to form elaborate networks of reactions that provide energy to the cell (metabolism), control cell division and cell differentiation, and perform other cellular functions.

The basic mathematics and physics of reaction-diffusion was worked out about a century ago by the Polish physicist Marian von Smoluchowski (1872-1917). In Smoluchowski’s time, modern computers did not exist. Calculations had to be performed by hand, paper and pencil, with at most primitive adding machines and slide rules. Modern computers make it possible to solve Smoluchowski’s mathematics for complex systems of tens, hundreds, even thousands of different chemicals reacting and diffusing inside the cells.

Marian von Smoluchowski

Smoldyn

Smoldyn, short for “Smoluchowski Dynamics”, is a free, open-source program for simulating reaction and diffusion in biological systems developed by biologist Steven Andrews and a few collaborators over the last decade. Smoldyn is available in both pre-compiled binaries for several systems and source code. With a few hiccups (installing the OpenGL 3D graphics and TIFF image libraries that Smoldyn requires) the author was able to build Smoldyn from source code in the cygwin environment on an Hewlett-Packard (HP) laptop running the Microsoft Windows 7 operating system.

Smoldyn Cell Simulation

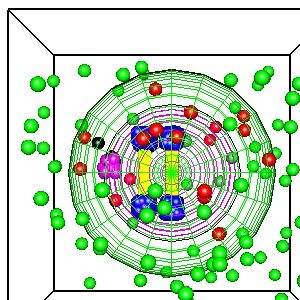
The illustration shows a simplified model of a cell with two chromosomes generated by Smoldyn using the OpenGL 3D graphics library. This is a simplified simulation of the “Bathtub Mechanism”, a possible cure for cancer that kills cells with an abnormal number of chromosomes.

The basic idea of the bathtub mechanism is an analogy to filling a bathtub with water (a cell killing poison) with multiple faucets (one for each chromosome) and a single drain with limited throughput. If there are too many faucets, too many chromosomes, the level of the water (the cell killing poison) will rise, overflowing the bathtub (killing the cell). If there is the normal number of chromosomes, the drain can remove the “water”, the cell killing poison, and the water level does not rise.

In the illustration, the green spheres represent a harmless precursor, a blockbuster drug :-). These diffuse inside the cell and react with the telomeres, the ends of the chromosomes which have a specialized chemical structure, illustrated by the blue spheres. The green cells react with the blue spheres to form the red spheres, the cell killer. The magenta spheres are the “drain” which converts the red spheres, the cell killer, to the black spheres, a harmless protein that the cell can safely digest or excrete. In cells with too many chromosomes, the concentration of the red spheres, the cell killer, will rise to lethal levels.

This is one example of how Smoldyn or other programs that simulate cell chemistry may be used to simulate complex chemical reactions that may be able to identify cancer cells and either selectively kill the cancer cells or inhibit their deadly behavior, perhaps independently of the confusing and daunting plethora of cancer genes. The abnormal number of chromosomes is found in many cancers with many different sets of mutated cancer genes.

But is the molecular transportation in cells caused by diffusion?

Biologists and other scientists typically model chemical reactions in cells with diffusion. Molecular biology has revealed astonishingly complex and sophisticated systems in cells. Chromosomes, for example, separate and divide in cell division in a complex, highly controlled fashion that neither looks nor sounds much like diffusion. Indeed biologists appear to believe that certain molecular systems function as tiny motors, pulling the chromosomes apart in a complex controlled fashion.

Conceptually, it is difficult to reconcile the slow, random process of diffusion with the many remarkable functions that have been found in the cell. The cell in many ways looks more and more like a sophisticated machine or computer, none of which operate based on diffusion. Are molecules somehow propelled or directed to specific places like packets in the Internet or electrical signals in an integrated circuit, by some as yet unknown and unimagined physical process?

Some mechanism for molecular transportation other than diffusion seems like a definite possibility to the author. Any models based on reaction and diffusion need to be carefully tested and compared with reality to see if indeed reaction and diffusion is the correct model for molecular transportation and chemical reaction in the cell.

Scope and Difficulty

For some reason, people tend to grossly underestimate the scope and difficulty level of mathematical software projects such as simulating cell chemistry. Although cost and schedule underestimation occurs in many areas of software development, it seems to be particularly common and particularly extreme in mathematical projects.

Some general comments. Experiences in high school and college math classes are misleading. Teachers and professors typically present example calculations or derivations of theorems that are relatively short and simple, taking a few hours of total class time, and covering a dozen blackboards or dry erase boards at most. These often correspond to the building blocks of the much more complex solutions to real-world problems or cutting edge research problems. The math in Smoldyn, for example, is equivalent to thousands of blackboards filled with equations and calculations.

In addition, in classwork, a performance level of 99% correct is usually exceptional, excellent work, an A+. In most real world applications, higher levels of correctness are needed, typically 99.9% (one error per thousand lines of computer code). Many specific errors are unacceptable. In aviation and rocketry for example, there are several cases where a single mathematical error in one line of code out of tens of thousands, resulted in the loss of a hundred million dollar plus mission. NASA’s Mars Climate Orbiter mission to Mars was lost in 1999 due to an improper conversion between English units (feet and pounds as a measure of force) and the metric system (meters and Newtons). Thus, much more time and effort is needed in real-world applications to eliminate all or most errors from real-world mathematics.

The core simulation engine of Smoldyn is about 25,000 lines of code. Even a single error can produce a fatal end result. How would you feel flying an airplane or taking a drug designed with a mathematical simulation that was only 99% correct?

According to the Smoldyn web site, Smoldyn represents about ten years of effort mostly by biologist Steven Andrews and his collaborator Nathan Addy. Smoldyn is not completed and does not yet fully simulate, for example, tubular structures such as chromosomes or the tiny filaments, microtubules , found throughout cells. Smoldyn does partially simulate simple cylinders used for chromosomes in the illustration, but the detailed mathematics does not accurately model molecules bound to the surface of the tubular structures, obviously a significant limitation since cells contain many such structures.

Conclusion

Simulation of cell chemistry may solve many pressing problems in health and medicine, including cancer. Current mathematical models and simulations of cell chemistry are based on the reaction-diffusion theory of cellular chemistry. Smoldyn is an example of a free open-source computer program that simulates cell chemistry based on the reaction-diffusion theory. The Bathtub Mechanism is a possible cure for cancer that can be simulated with Smoldyn and the reaction-diffusion theory of cell chemistry.

It is important to confirm that the reaction diffusion theory of cell chemistry is correct and predictive since many of the remarkable functions of cell are difficult to reconcile conceptually with the generally slow, random process of diffusion. Mathematical modeling and simulation of cell chemistry is a substantial and technically difficult undertaking, typically requiring anywhere from six man-months to many man-years of effort. The benefits may include cures or effective treatments for many diseases including cancer, arguably trillion dollar markets in some cases.

Credits

The picture of Marian von Smoluchowski is from Wikipedia; it is reportedly in the public domain as the copyright has expired.

The picture of the Smoldyn output was generated by the author.

Additional Resources

Animations of a Possible Cure for Cancer

The Magical Mathematics of Numb3rs

© 2012 John F. McGowan

About the Author

John F. McGowan, Ph.D. solves problems using mathematics and mathematical software, including developing video compression and speech recognition technologies. He has extensive experience developing software in C, C++, Visual Basic, Mathematica, MATLAB, and many other programming languages. He is probably best known for his AVI Overview, an Internet FAQ (Frequently Asked Questions) on the Microsoft AVI (Audio Video Interleave) file format. He has worked as a contractor at NASA Ames Research Center involved in the research and development of image and video processing algorithms and technology. He has published articles on the origin and evolution of life, the exploration of Mars (anticipating the discovery of methane on Mars), and cheap access to space. He has a Ph.D. in physics from the University of Illinois at Urbana-Champaign and a B.S. in physics from the California Institute of Technology (Caltech). He can be reached at jmcgowan11@earthlink.net.