Some readers may be familiar with Bob Palais’ article “π Is Wrong”. Within it Palais argues that π is the wrong choice of circle constant. This quote, from the author’s website, summarizes his main argument:
As noted in the last page of the pdf, I suggest calling the alternate constant 2 π=6.283… `1 turn’, so that 90 degrees is `a quarter turn’, just as we would say in natural language. The main point is that the historical choice of the value of π obscures the benefit of radian measure. It is easy to see that 1/4 turn is more natural than 90° , but π/2 seems almost as arbitrary. It is apparent that we can’t eliminate π but it is to be aware of its pitfalls, and introduce an alternative for those who might wish to use one.
— Bob Palais
Palais then goes on to define a “newpi” symbol through a TeX macro, which resembles the fusion of two π:

The aforementioned article has been in print since 2001, and very little has changed on this front since then. The ideas it put forth are an amusing opinion that many of us tend to agree with, but 2π has not been adopted by the mathematical community.
Today Michael Hartl announced “The Tau Manifesto” on what he calls Tau Day (6/28 for 6.28…). In this document, Hartl echoes the good points that Palais made and builds upon them to construct a strong case in favor of adopting a circle constant which is the ratio of a circle’s circumference to its radius, not its diameter. Inspired by Palais’ use of the word “turn”, he proposes calling this constant τ (tau).
As Hartl argues, this symbol already exists (unlike the odd symbol that Palais introduced), it’s still generally available in mathematics, and it resembles π.
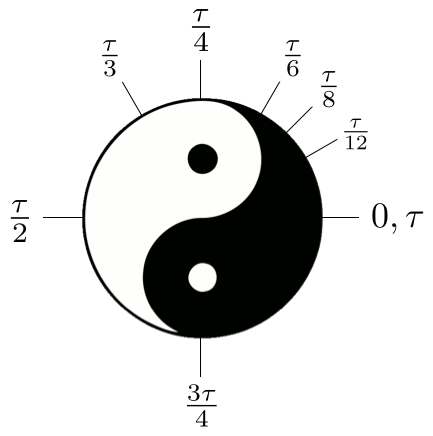
This new constant would not only be an improvement from a pedagogical standpoint (as shown in the diagram above), but would also “improve” several formulas. For example, Euler’s identity:
[tex]\displaystyle e^{i\pi} + 1 = 0[/tex]
Or:
[tex]\displaystyle e^{i\pi} = -1[/tex]
Which would become neater as:
[tex]\displaystyle e^{i\tau} = 1[/tex]
This makes sense intuitively (a rotation in the complex plane by one turn is 1).
(The Tau Manifesto addresses the issue of how this too can relate to the “five most important numbers in mathematics” with a slight rearrangement.)
What are your thoughts on this? As mathematics evolves, is it time to start using “Let τ = 2π” as a means of adopting a better circle constant?
I like the idea but I really doubt it’ll ever become mainstream.
I have conducted a personnal survey: almost nobody in the real life knows what pi is, even if they always know its value by heart. So tau has its chance in the mainstream…
I liked Tau BEFORE it was cool.
Pi is there because it is the ratio between the diameter of a circle and it’s circumference. No one measures the radius of a circle, it makes much more sense to just measure how “wide” a circle is.
Jordan, then why do we have [tex]C = 2 \pi r[/tex] and [tex]A = \pi r^{2}[/tex]? 🙂
I’m saying physically measuring it. That’s why it’s C = pi * d
Measuring the radius is harder than measuring a diameter. And the area formula works out better with pi and not this tau thing.
Actually, 1/2 tau r^2 is more “natural” than the current formula. It has more in common with familiar formulas such as 1/2 m v^2 etc.
Hardly. 1/2 tau r^2 makes it clear that you’ve got a triangle. There’s always a 1/2 with triangles.
that would make for a symbollic type of relationship seeing as if you draw circle inside of a triangle inside of a circle (where the perimeters of each inner shape symmetrically intersect 3 times) the relationship between the 2 circles is a 2:1 diameter.
How is measured the radius any harder than measuring the diameter. In both cases, you need to find the centre. If you just draw a line across a circle, you’ll get a chord which likely isn’t the diameter.
Take a look at digital calipers to understand why measuring a diameter can be easier than measuring a radius. That said, once you measure the diameter, you have the radius. Dividing by 2 is easy.
But you sketch a circle with its radius, not diameter. All formulae for circles and spheres etc. are in terms of r, and when considering aplications such as circular motion in physics the radius is more important than the diameter.
Tau is a bad symbol for this. Two situations where tau is used, torque and time constants, make frequent use of pi.
Also shearing stress is tau…might not be the best symbol used?
my god!!
THEN TODAY IS TAU DAY!! (6/28) !!
The way I learned about radians back in PreCalculus was that 1 radian was the angle on the unit-circle such that the arc along the circle across that angle is of length 1.
I didn’t (and still don’t) think of radians in terms of PI. I think of radians in terms of radii and arcs. PI is a nice convenient fact to remember about the radii and arcs.
This would also make many physics equations more intuitive. There are many times where the constant 2(pi) appears, and far fewer where (pi) is by itself.
I’m all for it. Pragmatism++
My colleague Andrej Cherkaev likes to point out that rather than an inscribed triangle, an inscribed hexagon (or 6 equilateral triangles of side 1) gives a very natural estimate for the circumference being close to, and slightly greater than 6 times the radius. ( Andrej and Elena have a very fun Math Jokes page:
https://www.math.utah.edu/~cherk/mathjokes.html
as well as nice pages on their interesting work on non-convex variational problems and composite materials:
https://www.math.utah.edu/~cherk/mathmat/index.html
https://www.math.utah.edu/~elena/ )
If it’s truly useful it will be adopted. The wonderful thing about mathematical reasoning is that there is nothing inherently wrong with setting tau = 2*pi and using some symbol for tau. If it helps convey reasoning, there is no mathematical precedent which forbids you setting the above relationship. Whether or not it is more ‘organic’ in terms of teaching math, I do not know. I think any apt math pupil would not be thrown by either interpretation, and there is no reason to redefine trig functions in terms of tau under the assumption that it would help the average student who only cares for the bare minimum of a passing grade in math.
Also, just would like to add: defining a constant tau=2*pi in no way ‘does away with’ the irrational constant pi, for tau is a multiple of pi. We strive to get at the most basic building blocks of geometric shapes, and pi is there whether we like it or not. This really seems to be an aesthetic issue/argument, IMO.
Then again, you could say that pi is a multiple of 1/2 pi, and 1/2 pi is the most basic building block.
I would vouchsafe that the guy who suggested this is a deluded math educator trying to make a name for himself who does not understand the difference between number and numeral.
hello, greetings to all …
my name is jose I’m Chilean and student teachers in mathematics, surfing the net I found this blog and my attention this post. I find great idea, this would bring super positive consequences for teachers of mathematics, since it is my hard to understand why many students circle the circumference is 2 pi, after which they are taught that the perimeter of a circle is 2 pi plus radio, this brings many Confucianism for students and makes us very difficult to make classes.
I am in favor of the change from pi to tau.
I’m with Bob Palais on this subject. For decades I have followed a simpler method of machine monitoring and control. Numerical methods are troublesome due to irrationals such as Pi. Software methods are equally troublesome. Fortunately there is an simpler, safer, and faster method that can be read about on scribd: “Natural Machine Logic.” “Software is Mostly Unnecessary” and the “Impediments of Computation” are sometimes too much to bear.
Charles Moeller
Interesting, but there are certainly more serious syntactical problems to worry about, such that milions of young programmers believe == is the generally accepted symbol for equality, and becomes confused when it is written = in mathematics…
It’s only a matter of time before this misconception has confused enough people to make this a real mess.
(This is due to the fact that thoughless programming language designers (of java, C# etc) included also the most perverted ad-hoc syntactical element of the primitive C-language (elements that originated from a really simple hack called B).)
Sven: Right! I propose mathematics adopts == as the proper equality symbol to correct this misconception.
Alternately, you could always convert people to Pascal, where := is an equality check, and = is an equality assignment.
Thats backwards. := is assignment in Pascal.
Unambiguous:
Pascal style assignment :=
C style comparison ==
Ambiguous:
Pascal style comparison =
C style assignment =
Of course APL has more characters and that’s another way to avoid ambiguity.
I agree completeley with Michael Hartl
Pi times the radias squared is the area of a circle
Tau times the radias squared devided by 2 is the area of a circle.
Pi makes things simpler.
If there was a way for Tau to find its way in middle school math (i.e. Algebra I and below) then I would use it. So far, I just fill it in when I see something. Like the Surface Area of a cylinder (2(pi)(r^2))+2(Pi)rh= T(r^2)+Trh
That is not simpler.
Can you easily understand why that is the area of a circle by looking at the formula?
A circle can be seen as a set of rolled up triangles. The area of a triangle is ½ * base * height. So a circle is ½ * circumference * radius. The circumference is tau * radius, so the area is ½ * tau * radius² which is far more clear and relatable to the triangle.
Removing the ½ in favor of the more obscure pi makes it harder to teach /why/ the formula for the area of a circle makes sense.
Also, it obscures an important pattern.
½ * c * a²
This is a very common formula pattern where c is a constant (like the circle constant, tau or pi).
You find it in the area of a circle: ½ * tau * radius²
You find it in kinetic energy: ½ * mass * velocity²
Mass is constant in this formula.
You find it in potential energy of a spring: ½ * k * x²
Where k is the spring constant, and x is the distance the spring is compressed or stretched.
You find it in the distance formula for motion: ½ * a * t²
This holds when the initial velocity and position is zero, and a is acceleration, which is constant in this formula, and t is the time during which the object has traveled.
And on and on and on…
And there’s A = 1/2∫r^2 dr
For a more detailed explanation about why ½ * tau * radius² is better:
https://sites.google.com/site/taubeforeitwascool/
I have been teaching math for over 20 years and I am finding this Tau fact very interesting.
It simplifies many concepts i.e. trig functions and graphs as shown in many videos. Also when the concepts of trig with radiants are presented, we often refer to the unit circle (with a radius of one) and not the 2-circle with a diameter of 2.
I am a big tau supporter now..
but i thing most people in the world more familier with PI than with TAU. and its more comfortable to use PI nowadays as we are using PI from olden days itself.
In what way is π more confortable?
Sorry but at work coffee pause is at Pi (15h14), and Tau time is really to late for coffee
So your coffee break is at tau/2, no problem, halfway there.
Mmmh, hard question …
I don’t like the general spirit around pi & tau
Too much agressif about pi ! Pi isn’t wrong, pi isn’t bad !! Finaly, tau = 2pi … nothing more !
I agree, tau is interesting for teaching ! So more simple tu speak about “1 turn” and not “2 half of a turn”
And interesting too, for some radian compute or concept !
I agree to officialize tau, and can teach it.
BUT:
Pi constant, isn’t too be replaced by tau.
Both can coexist, simply.
Wanting to supress pi, is just extremist !
Depending what you do with the “circle constant”, pi is sometimes better than tau !
For exemple, it could seems stupid, but it’s the same “war of tau”
Why tau ? Because it is one turn ! More simple !
Ok, but what about the angles representation ?
If you can easily, mentally, compute radians, you never need pi or tau.
Infact, we can’t do this easily, then we do fraction on “these” constants.
The more simple fraction to do, is 1/2 … so easy !
The next one is 1/4 … yes easy again, the half of an half …. we all see it !
1/8 … ok, we can abord it quikly … but it become less easy.
1/16 .. still ok but it is, for me, the limit of my “direct intuitive comprehension”, no infact it is already too much.
1/32 … too hard … i need too think, and I don’t represent it !
With tau, we can directly represent tau/8 it’s equal at 45°
With pi, we can directly represent pi/8 it’s equal at 22.5°
Tau / 16 … I need to think … a short time, but I need too think.
If you want, via tau, simplify the mental process. Don’t forget pi, he is sometime better !
Then, back to the question, what too teach and use ? Pi or tau ?
I don’t realy know.
Personaly, for teaching I prefer tau, for using I prefer pi.
Just let both exist ! And use the more practice for you.
I like the both !
Fab.
Letting both exist is confusing. π needs to die!
Storm in a teacup. Pi is better with regard to almost anything; it is simpler, for a start. 2xPi is just 2xPi. The fact that it makes trivial radian angle a tiny bit more trivial should not mask the fact that it makes areas more complicated (the area of a unity circle is Pi; how simple is that?), and is wholly unneeded to begin with. “Tau” is just a multiple of Pi.
The only people who care about “tau” are the people who can’t multiply by 2 (but stangely enough, can divide by 2, apparrently). SOME mathematicians…
I can see C = (Tau)r, but what about area of a circle formula – you would just have to have 1/2(tau)r squared and that kind of defeats the point
Many other formulae are in the same sort of form as 1/2tau r^2,
for example Ek = 1/2mv^2
E = 1/2kd^2
and A = 1/2∫r^2 dr etc.
I think there are more important mathematical concepts to muddy the brain with than whether we double or half pi to make it make more sense. Also, I’m an extremely biased pi zealot.
The idea is interesting, but I do not believe it will become popular. Everyone is so familiar and comfortable with pi. Pi is also related to almost everything around us. Anything with a circle has a circumference of roughly 3.14. It would be too much of a change for people to move on from pi. However, tau is more simple because it is only one turn as opposed to two. I just think it would be too much of a change for pi since most people are comfortable with pi, and we all know most people do not like change.